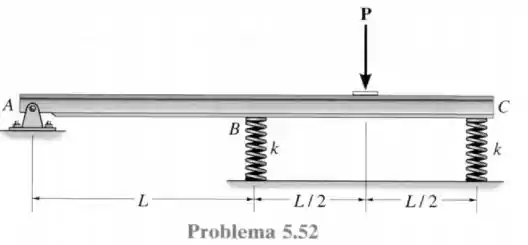
52- A viga não flexível de peso desprezível é apoiada horizontalmente por duas molas e um pino. Considerando que as molas não estão deformadas quando a carga é removida, determine a força em cada mola quando é aplicada a carga . Calcule também a deflexão vertical da extremidade . Considere que a rigidez da mola é grande o suficiente de modo a permitir apenas pequenas deflexões. Dica: a viga gira em relação ao ponto e as deflexões nas molas podem ser relacionadas.
Passo 1
Por ter três apoios e apenas uma força essa viga é do tipo hiperestática e para isso precisamos utilizar de um artifício interessante que será mostrado mais a frente.
As molas fazem uma reação na viga de forma que temos o seguinte diagrama de forças abaixo:
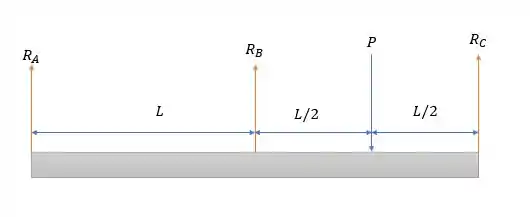
Vendo que não há forças ativas na horizontal conseguimos deduzir que não há reações na horizontal em .
Passo 2
Fazendo a somatória das forças verticais temos:
E fazendo a somatória dos momentos em :
O que nos mostra que precisamos de alguma outra relação que interligue e , para isso precisamos utilizar a propriedade das molas.
Por girar em torno de e as duas molas estarem ligadas por uma reta podemos desenhar o seguinte deslocamento.
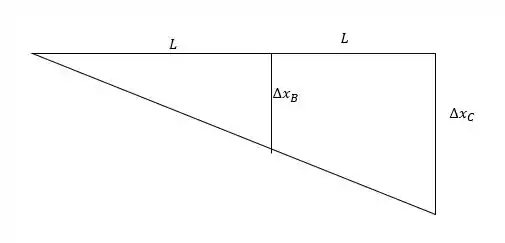
Então por semelhança de triângulos temos que:
Passo 3
Da lei de Hooke temos que:
Logo :
Então:
Logo será:
E a deflexão será: