Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 4.4 - Ex. 9

4.9. Determine a intensidade, a direção e o sentido do momento resultante das forças em relação ao ponto P.

Passo 1

Vamos começar esquematizando o problema.

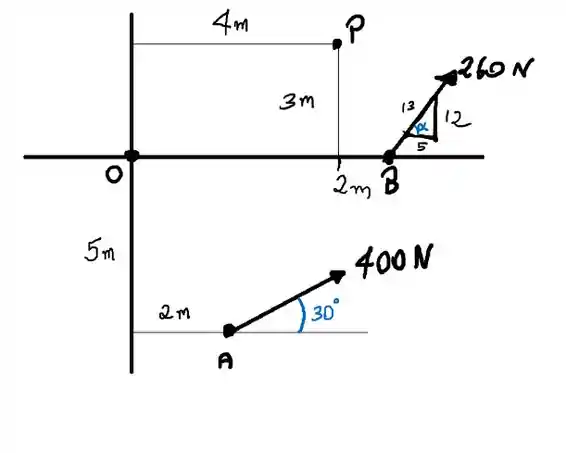
O momento resultante é a soma dos momentos.

Então

M = M A + M B

Passo 2

Vamos começar calculando M A

M A x = 400 ⋅ cos ⁡ 30 ° ⋅ 8 = 2771,28   N ⋅ m

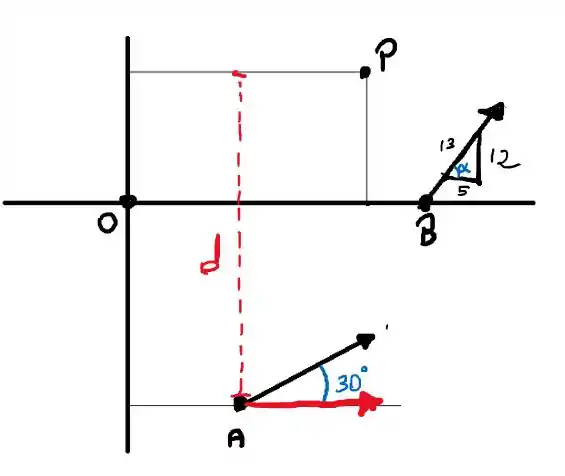
E

M A y = - 400 ⋅ sin ⁡ 30 ° ⋅ 2 = - 400   N ⋅ m

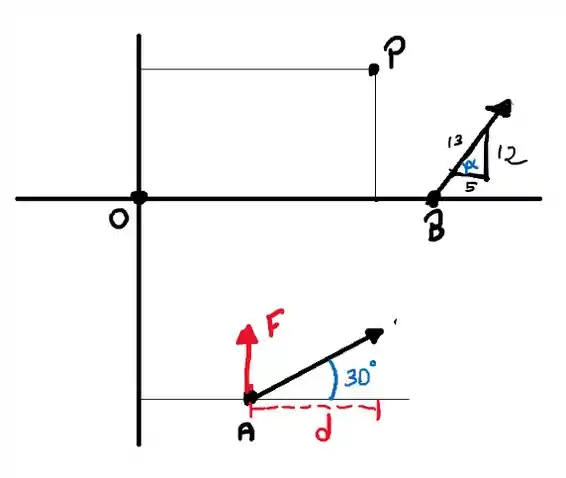
Então

M A = 2771,28 - 400 = 2371,28   N ⋅ m

Passo 3

Agora M B

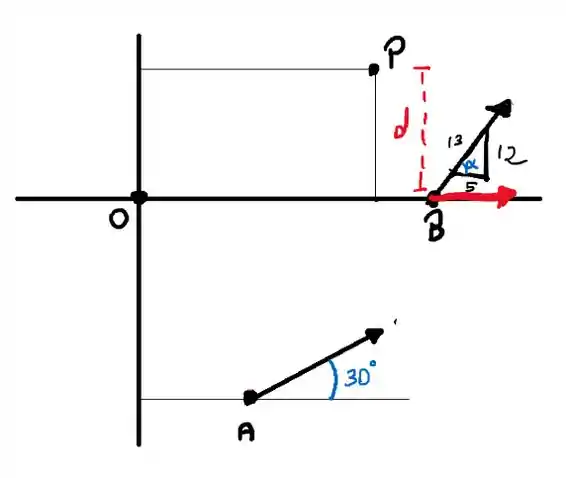
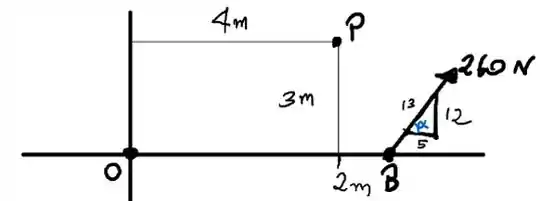
A componente horizontal da força é ( 260 ⋅ cos ⁡ α )   e o momento que ela faz é esse valor multiplicado pela distância perpendicular, ou seja, a distância vertical 2:

M B x = 260 ⋅ cos ⁡ α ⋅ 3

A componente vertical da força é ( 260 ⋅ sin ⁡ α ) e o momento que ela faz em P é:

M B y = 260 ⋅ sin ⁡ α ⋅ 2

Pelo triângulo, temos

s en ⁡ α = 12 13

cos ⁡ α = 5 13

Então

M B x = 260 ⋅ cos ⁡ α ⋅ 3 = 260 ⋅ 5 13 ⋅ 3 = 3 00   N ⋅ m

M B y = 260 ⋅ sin ⁡ α ⋅ 2 = 260 ⋅ 12 13 ⋅ 2 = 20 80   N ⋅ m

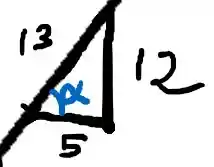
Então, como ambos são no sentido anti-horário, ou seja, positivo, é só somar:

M B = 2380     N ⋅ m

Passo 4

Agora podemos determinar M

M = M A + M B

M = 2371,28 + 2380 = 4751,28   N ⋅ m

M = 4,75   k N ⋅ m

Resposta

M = 4,75   k N ⋅ m

Seu sentido é anti-horário.

Ver Outros Exercícios desse livro