51- O comutador com ação de cotovelo consiste em uma alavanca que é presa por pinos a uma estrutura fixa em e mantida numa dada posição por meio da mola, que tem comprimento de quando relaxada. Determine a intensidade da força resultante em e a força normal na cavilha em quando a alavanca está na posição mostrada na figura.
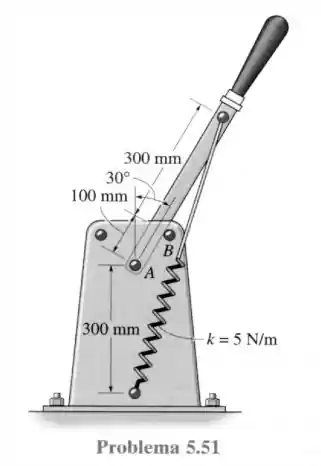
Passo 1
Dicionário: Uma cavilha é um uma pequena peça cilíndrica, normalmente de madeira, plástico ou metal. Se for em madeira poderá chamar-se também tornel. É usada em inúmeras aplicações, sobretudo como suporte e elemento que confere resistência mecânica em uniões de peças de madeira ou metal
Resumindo a cavilha em é o que vai parar a alavanca, mas antes de nos preocupar com essa força de parada , vamos calcular a força elástica nesse mola pela geometria formada por essa comutadora.
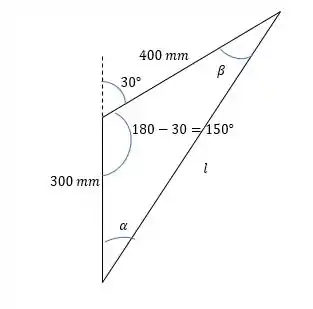
Pela lei dos cossenos temos:
Isso faz com que a força elástica seja de:
Outra coisa importante de se descobrir são os ângulos desse triângulo que serão:
Que pela lei dos senos serão iguais a:
Passo 2
Agora vamos traçar o diagrama de forças na alavanca.
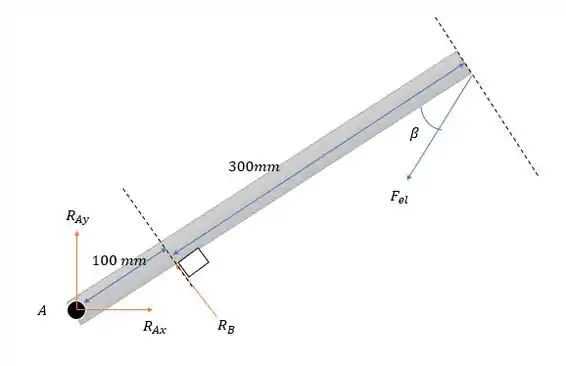
Fazendo a somatória dos momentos em temos:
Passo 3
Agora vamos redesenhar a figura do passo anterior um pouquinho para que seja mais fácil calcular as reações em .
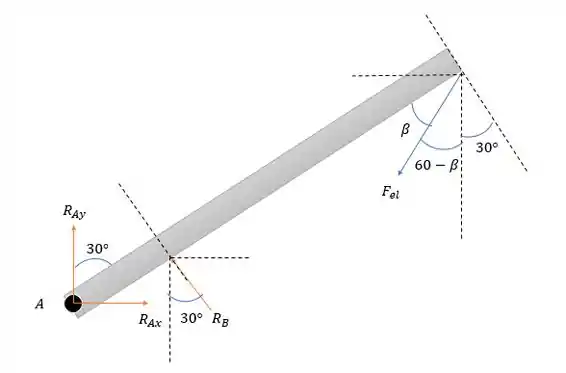
Fazendo a somatória das forças verticais temos:
E a somatória das forças horizontais será:
Logo a resultante em será: