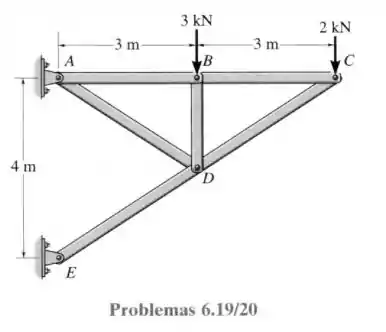
20- Cada elemento da treliça é uniforme e tem massa por unidade de comprimento de . Remova as cargas externas de e e determine a força aproximada em cada elemento devido ao peso da treliça. Indique se esses elementos estão sob tração ou compressão. Solucione o problema admitindo que o peso de cada elemento pode ser representado como uma força vertical, metade da qual é aplicada nas extremidades de cada um dos elementos.
Passo 1
A barra tem comprimento de e por conta disso o peso dessa barra valerá:
E com isso metade desse peso estará no nó e a outra metade no nó . Com isso as forças em cada barra serão iguais a:
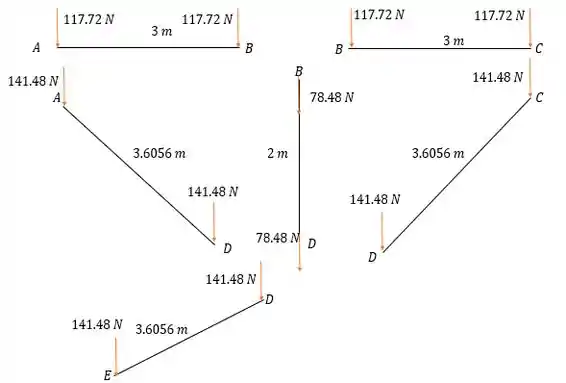
Isso já deixa a nossa estrutura com o seguinte carregamento.
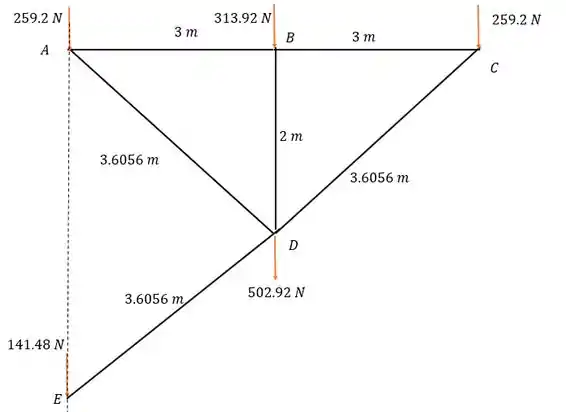
Passo 2
Agora podemos analisar nó por nó e descobrindo as forças em cada barra.
Analisando as forças no nó .
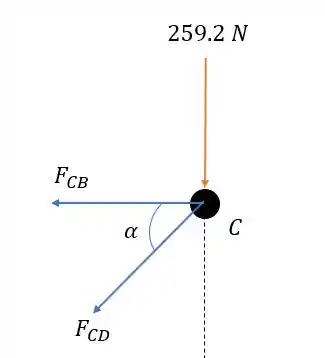
Onde vale:
A somatória das forças verticais valerá:
Força compressiva.
Agora vendo a somatória das forças horizontais:
Passo 3
Agora analisando as forças no nó .
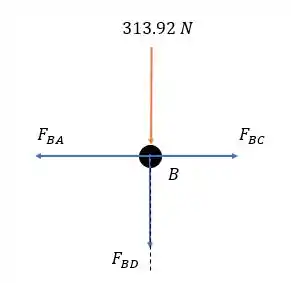
Fazendo a somatória das forças horizontais temos:
Agora fazendo a somatória das forças verticais:
Força compressiva.
Passo 4
Agora para o nó .
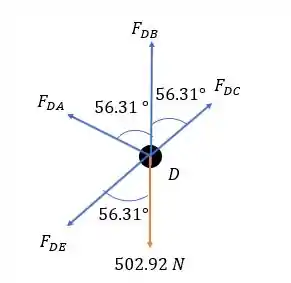
Da questão anterior podemos exportar os ângulos que encontramos lá:
Substituindo os valores temos:
E fazendo a somatória das forças horizontais:
Com essas duas equações temos:
Força compressiva.
Logo:
Força trativa.