Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 54

5/54) Mostre que as expressões v = r ω e a t = r α , são válidas para o movimento do centro O da roda querola sobre o arco circular côncavo ou convexo , onde ω e α são a velocidade e a aceleração angular absoluta , respectivamente , da roda . (Sugestão : siga o modelo do exemplo 5/4 e permita que a roda role uma pequena distância . Tome muito cuidado em identificar o ângulo absoluto correto através do qual a roda gira em cada caso na determinação de sua velocidade angular e aceleração angular .)

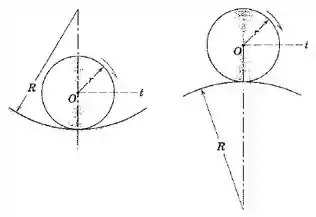
Passo 1

Então galera , para resolvermos este exercício , devemos lembrar da relação :

v = r ω = r θ '

Sendo assim , para o 1° caso , temos que :

v o = v = R - r θ '

R θ = r θ + β

Então ,

θ R - r = r β

θ ' R - r = r β '

Dessa forma ,

v = r β '   e   ω = β '

Portanto ,

a t = r α

( β = â n g u l o   a b s o l u t o )

Passo 2

Utilizando raciocínio análogo ao do caso anterior para o 2°caso , temos que :

v o = v = R + r θ '

R θ = r β

Então ,

θ + β = r + R r θ

Dessa forma ,

r θ ' + β ' = ( R + r ) θ '

Onde , ω = ( β ' + θ ' )

Sendo assim ,

v = r ω

Portanto ,

a t = r α

( β + θ = â n g u l o   a b s o l u t o )

Tranquilo galera? Bora resolver mais questões então!!!!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um volante de motor de 3.000 kg leva 10 minutos para desacelerar até o repouso a partir de uma velocidade angular de 300 rpm. Sabendo que o raio de giração do volante é de 900 mm, determine a intensid
Um quadro de 2 m é colocado em um caminhão com uma extremidade repousando sobre um bloco preso no piso e a outra apoiada em uma divisória vertical. Determine a máxima aceleração admissível do caminhão
Desenhe os diagramas de esforço cortante e de momento fletor da barra AB do Problema 16.17.PROBLEMA 16.17 Três barras, cada uma de massa de 4 kg, são soldadas juntas e unidas por pinos a duas hastes d
Um sistema de transporte é equipado com painéis verticais, e uma barra A B de 300 m m e de massa 2,5 k g é depositada entre dois painéis como mostra a figura. Se a barra permanece na posição mostrada
Um sistema de transporte é equipado com painéis verticais, e uma barra A B de 300 m m e de massa 2,5 k g é depositada entre dois painéis como mostra a figura. Sabendo que a aceleração do sistema é 1,5