Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 2
Um sistema de transporte é equipado com painéis verticais, e uma barra de e de massa é depositada entre dois painéis como mostra a figura. Se a barra permanece na posição mostrada na figura, determine a máxima aceleração admissível do sistema.
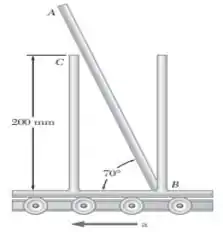
Passo 1
O exercício pede que a gente encontre a máxima aceleração admissível do sistema
Geometria.
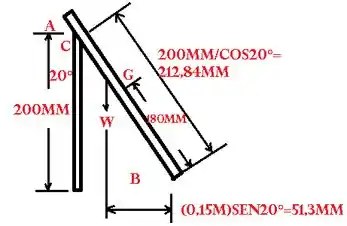
Peso
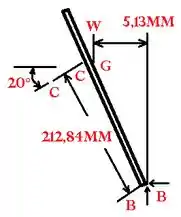
Passo 2
Aceleração máxima permitida.
Para
Para eq.(1),
Resposta
Exercícios de Livros Relacionados
Mostre que o sistema de forças efetivas para uma placa rígida em movimento plano é reduzido a um único vetor e expresse a distância do centro de massa G da placa à linha de ação desse vetor em termos
Uma força P de intensidade igual a 3 N é aplicada a uma fita enrolada em torno do corpo indicado na figura. Sabendo que o corpo repousa sobre uma superfície horizontal sem atrito, determine a aceleraç
(a) No Problema 16.48, determine o ponto da barra AB onde a força P deve ser aplicada para a aceleração do ponto B ser igual a zero. (b) Sabendo que P = 1 N, determine a aceleração correspondente do p
Uma barra delgada uniforme AB repousa sobre uma superfície horizontal sem atrito e uma força P de intensidade igual a 1 N é aplicada em A em uma direção perpendicular à barra. Sabendo que a barra tem
Uma força P é aplicada a uma fita enrolada em torno de um disco uniforme que repousa sobre uma superfície horizontal sem atrito. Mostre que para cada rotação de 360 ° do disco, o centro do disco se