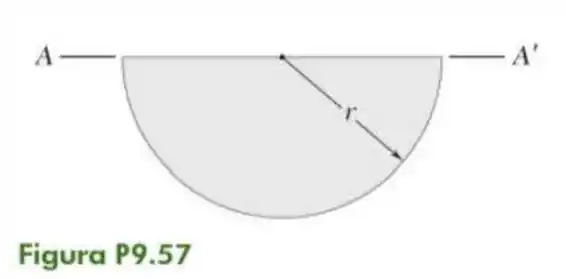
57- O painel mostrado na figura forma a seção transversal de uma calha que está cheia de água até a linha . Voltando a Seção , determine a profundidade do ponto de aplicação da resultante das forças hidrostáticas atuantes sobre o painel (o centro de pressões).

Da seção nós vemos que a intensidade das forças é dada por:

E a soma dos momentos será dada por:

E como força multiplicado pela distância é igual ao momento, então a somatória de todas as forças estará presente no ponto de atuação de tal forma que:

Onde é a distância até o eixo e que não necessariamente é no seu centro geométrico, pois a água forma uma carga triangular.

Porém a força resultante com certeza estará sendo aplicado no centro geométrico da seção transversal. (Só ver onde todo carregamento aplica sua força)