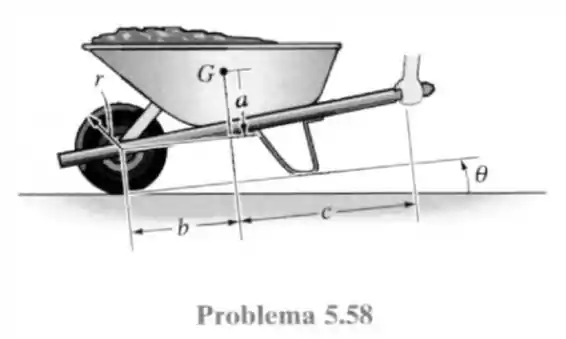
58- O carrinho de pedreiro e seu conteúdo têm em massa e centro de massa em . Determine o maior ângulo de inclinação sem deixar o carrinho tombar.
Passo 1
Desenhando o sistema de forças do carrinho temos.
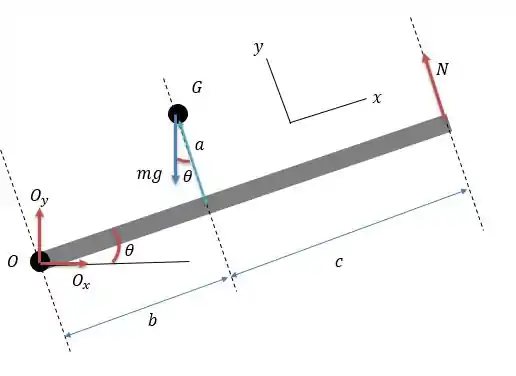
Onde é a força normal na mão do pedreiro que faz o carrinho ter uma angulação igual a . E o ponto representa o centro da roda.
Passo 2
A somatória dos momentos em nos dá:
Isso faz com que encontramos uma força normal na mão do pedreiro igual a:
Passo 3
Para descobrir o ângulo máximo que esse carrinho pode assumir basta fazer como que seja igual a zero. Pois aí temos a condição limite de tombamento do carrinho (ou seja, a hora que o carrinho perde o contato com a mão do pedreiro).