Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 58
58- O coeficiente de atrito estático entre o corpo de e a cunha com ângulo de vale . Determine o módulo da força necessária para levantar o corpo de se rolamentos com atrito desprezível estejam colocados sob a cunha como mostrado e os rolamentos sejam removidos e o coeficiente de atrito estático seja válido para essa superfície também
Passo 1
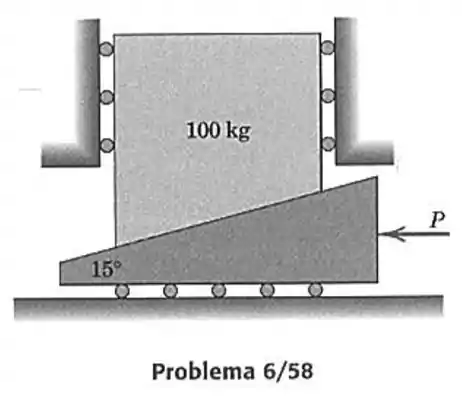
Para a letra somente teremos a influência da angulação da rampa no sistema tal como na figura abaixo:
O ângulo de atrito entre o plano e a massa é de:
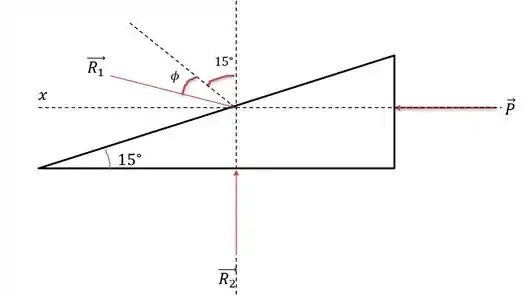
Onde é a reação da massa no plano e é a reação do plano no chão (como existe o atrito no plano com a massa temos a influência do ângulo de atrito na massa, como isso não existe com o plano e o chão não teremos esse ângulo de atrito). Para a massa temos as seguintes reações.
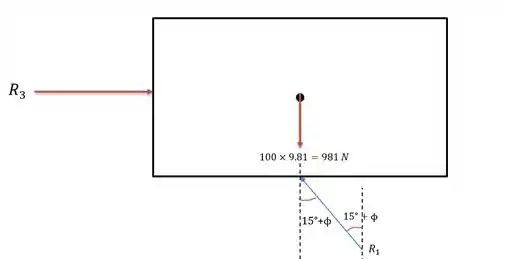
Passo 2
O que nos dá a soma das forças verticais igual a:
E por consequência podemos utilizar essa reação no calço para encontrar a somatória das forças horizontais:
Passo 3
Letra b) Como removeu os roletes no chão, surge uma reação de mesmo ângulo no chão para o plano tal como na figura abaixo.
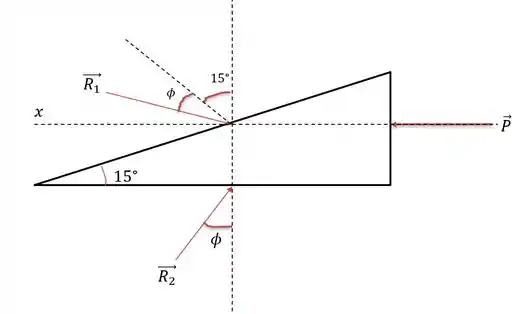
Enquanto o sistema da massa continua igual, logo .
Rebatendo essa força verticalmente nós teremos:
Logo será:
Agora fazendo a somatória das forças horizontais igual a zero:
O que faz com que seja:
Resposta
Letra a)
Letra b)