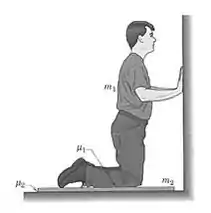
6/13) Uma pessoa ( massa m 1 ) ajoelhada em um painel de compensado (massa m 2 ) deseja se empurrar e ao painel para loge da parede à direita . Determine a condição sobre μ 2 que lhe permitiria fazer isto , em vez dele deslizar em relação ao painel estacionário . Os dois coeficientes de atrito estático aplicáveis são μ 1 e μ 2 . Avalie μ 2 para m 1 = 80k g , m 2 = 10k g e μ 1 = 0,60 .

Enunciado

Então galera , para impedir o deslizamento entre a pessoa e o painel , temos que aplicar a equação de equilibrio em relação a eles :

Utilizando raciocínio análogo ao procedimento anterior , para impedir o deslizamento abaixo de , temos que aplicar a equação de equilíbrio dada por :

Bom pessoal , analisando o problema por outra perspectiva , para o deslizamento ocorrer abaixo de , temos que :

Logo ,

Substituindo os valores que já conhecemos , obtemos que :

De boa galera? Então bora resolver mais exercícios como esse!