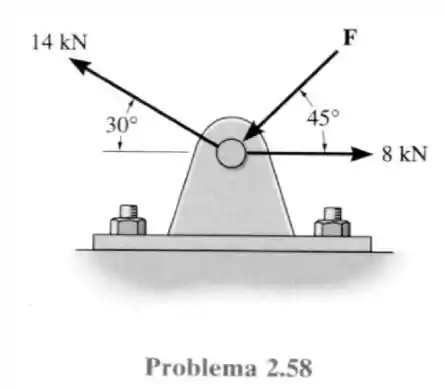
58- Determine a intensidade da força , de modo que a força resultante das três forças seja a menor possível. Qual é a intensidade da força resultante?
Passo 1
Vamos traçar os eixos e no ponto de aplicação das forças para que a gente consiga determinar o sentido das forças.
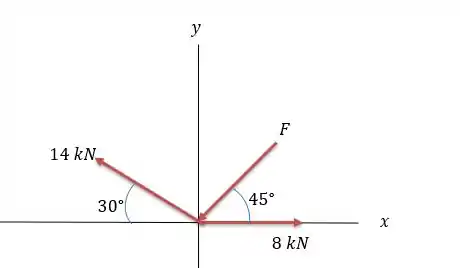
Passo 2
Logo fazendo a somatória das forças em temos:
E o somatório das forças em :
Logo a intensidade da força resultante será:
Passo 3
Se fizermos a derivada segunda da parábola dentro da função nós encontraremos um número constante positivo, logo a parábola terá concavidade para cima tendo um ponto de mínimo local. Logo se fizermos a derivada primeira e igualarmos a zero nós encontraremos o ponto de mínimo local:
Igualando a zero temos:
Passo 4
Substituindo na equação de encontraremos a intensidade da força resultante, então: