75- O elemento é sustentado por um cabo e em é sustentado por uma barra quadrada que se encaixa com folga através de um orifício quadrado na junta da extremidade do elemento, como é visto na figura. Determine os componentes de reação em e a força no cabo necessários para maneter o cilindro de em equilíbrio.
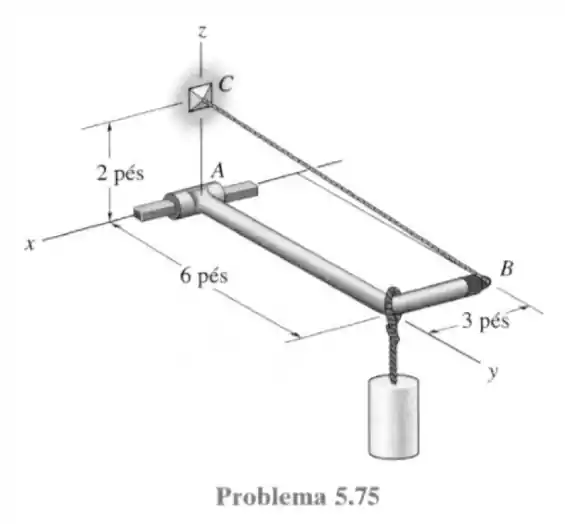
Passo 1
A junta oferece resistência de força e de momento em todos os eixos, então precisamos calcular todas elas.
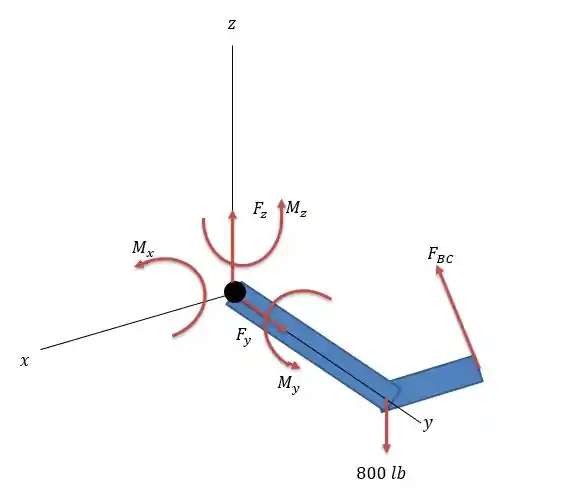
Onde a junta se move livremente em (informação deduzida por conta da folga no encaixe).
A força pode ser encontrado pela posição de e .
A posição de no sistema cartesiano é dado por:
E é:
Logo o vetor de direção é a diferença do ponto com o ponto e é:
E terá um tamanho total igual a:
Logo o vetor unitário será igual a:
O que nos dá um vetor força igual a:
Passo 2
A única força externa que existe no sistema é em logo fazendo a somatória das forças em temos:
Onde é o cosseno do ângulo diretor da força no eixo .
Com isso conseguimos dizer que pela somatória das forças em que
E pela somatória das forças em que
Passo 3
Agora vamos calcular as reações resistentes.
A força de gera um momento em pelo eixo de , multiplicando vetorialmente temos um momento em:
Sendo esse o .
Como não temos mais nenhuma força externa podemos dizer que: