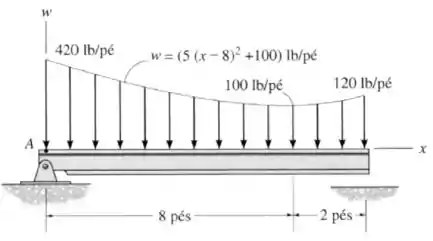
Determine a intensidade da força resultante equivalente da distribuição de cargas e especifique sua localização sobre a viga, medida a partir do ponto .
Passo 1
O primeiro passo para resolver essa questão é calcular a força total gerada por essa distribuição de forças. Para isso, precisamos integrar a função que foi dada na imagem:
Vamos simplificar um pouco essa expressão antes de integrá-la. Para isso podemos “abrir” aquele produto notável e somar tudo o que for possível:
Agora sim, ficamos apenas com a integrarl de um polinômio, então:
Beleza, já temos a intensidade da força resultanete.
Passo 2
Como fazemos para descobrir a localização em que essa força age na viga? Temos que calcular o momento da distribuição, e depois exigir que a nossa força resultante produza esse mesmo momento.
Então vamos lá, para calcular o momento da distribuição precisamos usar uma fórmula:
Onde é a posição de cada ponto em relação ao ponto :
Que é apenas a mesma integral que fizemos antes, mas multipicada por um a mais. Então vamos aproveitar a conta que fizemos lá em cima:
Agora é só resolver essa integral de polinômonio e substuir os limites:
Passo 3
Ok, então queremos que a nossa força de produza um momento de .
Isso quer dizer que a posição da força tem que satisfazer a seguinte equação:
E essa é a distância entre o ponto de aplicação da nosa força e o ponto .
Resposta
A força deve ter uma intensidade de e deve agir a uma distância de do ponto .