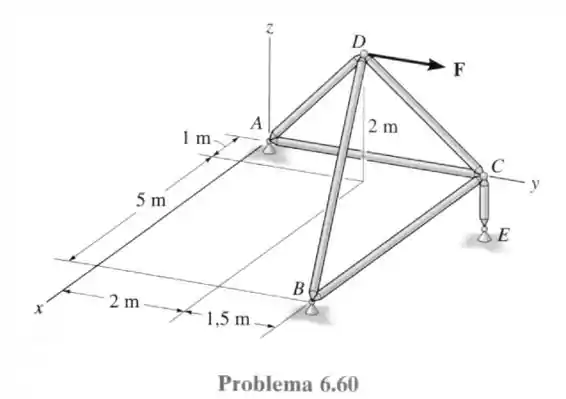
60- Determine as forças em cada um dos elementos da treliça espacial e indique se eles estão sob tração ou compressão. A treliça é apoiada por uma junta esférica em e . Considere que . Dica: a reação de apoio em atua ao longo dos elementos . Por que?
Passo 1
Da mesma forma que analisamos junta por junta uma estrutura nós também podemos fazer esse mesmo raciocínio para estruturas . A diferença é que deveremos somar as forças em três dimensões.
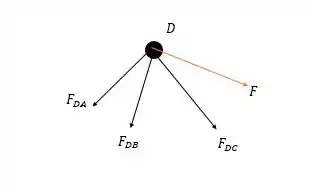
Vamos encontrar todos os vetores dessas forças pela posição dos pontos:
Agora tirando os vetores a partir dos pontos nós teremos:
E os vetores forças serão os vetores unitários multiplicados pela força ou seja:
Passo 2
Agora vamos fazer a somatória das forças em :
A somatória das forças em nos dá:
E a somatória das forças em :
Resolvendo esse sistema de três equações com três incógnitas nós teremos:
Passo 3
Agora vamos para a junta onde calcularemos as últimas forças.
O ponto está na posição:
E as outras estarão.
Onde pode ser qualquer valor.
Note que o ponto está no mesmo eixo em relação a o ponto está no mesmo eixo e o ponto está no eixo . Então basta rebater a força em relação a esses eixos com os ângulos diretores de modo que temos o seguinte diagrama de forças na junta.
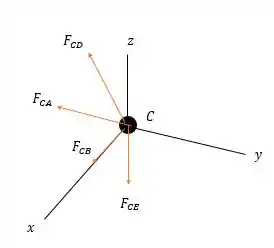
Fazendo a somatória das forças em temos:
Agora a somatória das forças em nos dará:
E a somatória das forças em :
Pois o sentido de é o oposto de , logo para realizar essas contas nós devemos inverter o sinal dos ângulos diretores.