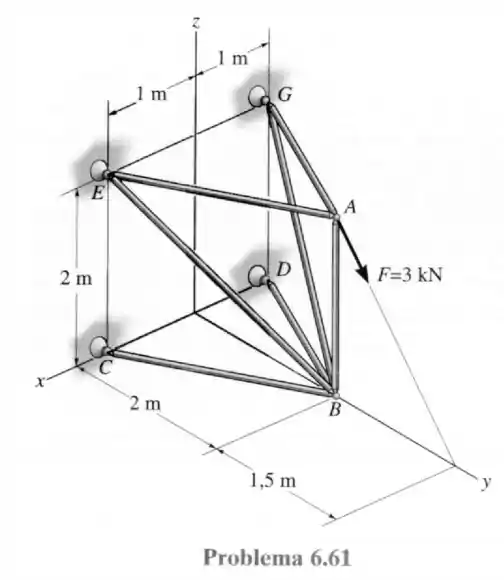
61- Determine as forças em cada um dos elementos da treliça espacial e indique se eles estão sob tração ou compressão. A treliça é apoiada por juntas esféricas em e .
Passo 1
Note que somente pelas forças na junta e na junta nós conseguimos encontrar as forças em todas as barras, e é isso que vamos fazer mas primeiramente vamos encontrar o vetor da força .
Cujo comprimento vale:
Logo como a intensidade desse vetor é de teremos um vetor força representado da seguinte forma:
Passo 2
Agora vamos fazer a somatória das forças na junta fazendo com que todas as forças saiam da junta em da seguinte forma:
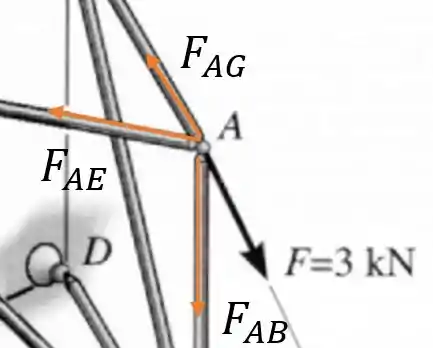
Dessa forma vamos encontrar as representações vetoriais de todas as barras.
Passo 3
Agora poderemos fazer a somatória das forças em todos os eixos.
Começando pela somatória das forças no eixo :
Como consideramos as forças saindo do nó então temos uma força compressiva nessa barra.
Agora vamos fazer a somatória das forças no eixo :
Logo para a somatória das forças no eixo :
Substituindo nós teremos:
Forças trativas.
Passo 4
Agora vamos para junta onde teremos o seguinte sistema de forças.

Onde
E as posições vetoriais das outras forças serão iguais a:
Pela simetria das barras e em x e y podemos dizer que elas terão o mesmo valor de força, além da simetria das barras em e . Além do fato que em e em não teremos nenhuma força resultante ou seja:
Passo 5
Fazendo a somatória das forças em nós teremos:
Agora fazendo a somatória das forças em :
Essa igualdade causada pela simetria pode ser encontrada fazendo a somatória dos momentos nos eixos e .