Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 5.4 - Ex. 62
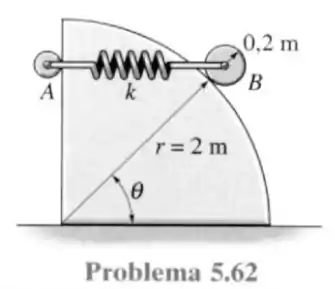
62- O disco tem massa de e permanece apoiado na superfície cilíndrica lisa por meio de uma mola de rigidez e comprimento não distendido . A mola permanecerá na posição horizontal, uma vez que sua extremidade em está presa ao pequeno rolete-guia, de peso desprezível. Determine o ângulo para o limiar de equilíbrio do rolete.
Passo 1
O cilindro faz uma normal no disco , além da força elástica que pode estar tendendo a comprimir ou a se fechar.
Considerando que a mola está esticada e quer se comprimir temos:
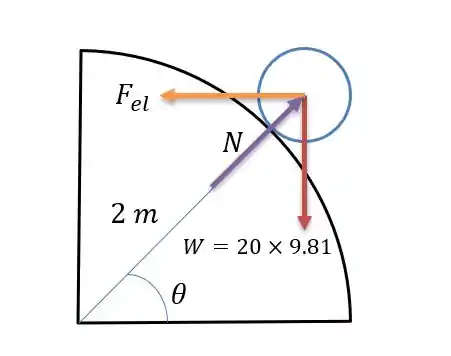
Fazendo a somatória das forças em temos:
Passo 2
Agora fazendo a somatória das forças em temos:
Substituindo o valor de que encontramos no passo anterior temos:
Dessa equação podemos tirar:
Passo 3
Porém da figura podemos tirar o cosseno do ângulo, onde a hipotenusa vale o raio do quarto de círculo mais o raio do disco e o cateto adjacente vale o alongamento total da mola, ou seja onde , logo:
Então podemos escrever:
Substituindo essa equação na equação que encontramos no passo temos:
Para essa equação dar certo teremos que ter:
