Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 1.9 - Ex. 3
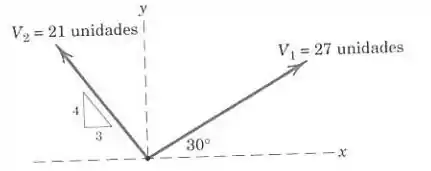
Para os vetores e do Prob. ½, determine o módulo da diferença vetorial e o ângulo que faz com o eixo positivo . Complete tanto a solução gráfica quanto a algébrica.
Passo 1
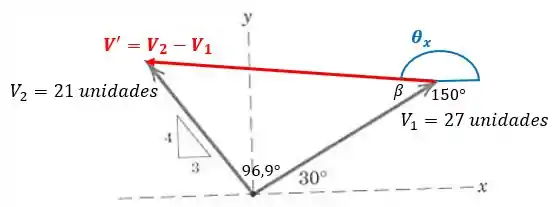
Graficamente, a diferença vetorial , é o vetor que se origina na “ponta” de até a “ponta” de . Os três vetores formam um triângulo, como mostrado na figura. E o ângulo que V’ faz com o eixo positivo x é o mostrado em azul na figura.
Passo 2
Beleza! Agora vamos fazer a solução algébrica, usando a lei dos cossenos:
Para determinar , primeiro calculamos o ângulo por meio da lei dos senos:
E assim:
Resposta
Exercícios de Livros Relacionados
Determine a intensidade da força resultante F R = F 1 + F 2 e sua direção, medida no sentido horário a partir do eixo u positivo.
Decomponha F2 nas componentes que atuam ao longo dos eixos u e v e determine suas intensidades.Fonte: Estática Mecânica para Engenharia – 14ª ed
Determine a intensidade e a direção da resultante F R=F 1+F 2+F 3 das três forças encontrando primeiro a resultante F ’=F 1+F 2 e depois formando F R=F ’+F 3 .Fonte: Estática Mecânica para Engenharia
Duas forças atuam sobre o parafuso de argola. Se F 1 = 400 N e F 2 = 600 N, determine o ângulo u ( 0 0 ≤u ≤180 0 ) entre elas, de modo que a força resultante tenha uma intensidade F R = 800 N.
Determine a intensidade e a direção da força resultante F R medida em sentido anti-horário a partirdo eixo x positivo. Resolva o problema encontrando primeiro a resultante F ’=F 1+F 2 e depois formand