62- Determine a intensidade e os ângulos diretores coordenados da força resultante.
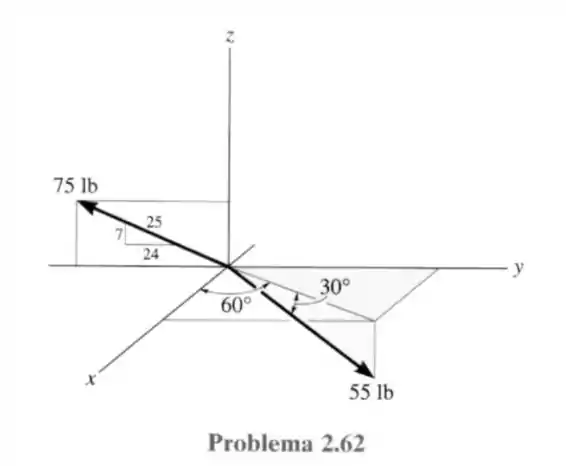
Passo 1
Ás vezes o desenho pode não ficar muito claro para a gente principalmente na hora de uma prova, então vai uma descrição básica a força de está situada apenas no plano com negativo e a força de está com um ângulo de abaixo no eixo de , logo espelhando a força de temos:
Uma vez o ângulo formado entre a reta e o eixo tem cosseno igual a e o seno vale .
Para representar a força de primeiramente temos que espelhar essa força no plano para depois encontrar suas componentes no eixos e . Esse raciocínio nos dará o seguinte vetor.
O que nos dará o vetor igual a:
Passo 2
Somando as duas forças temos a força resultante, que será:
Logo a intensidade dessa força será igual a:
Passo 3
Agora podemos encontrar os ângulos diretores pelas fórmulas.
Onde é a componente do vetor .
Continuando:
E: