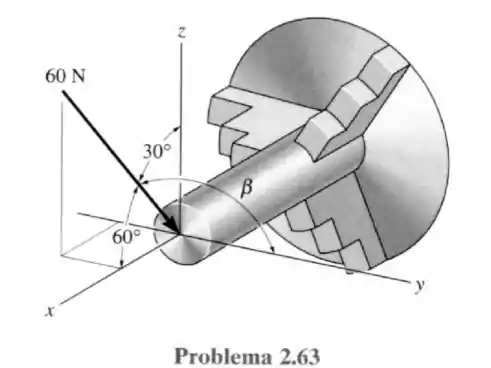
63- O tarugo montado no torno está sujeito a uma força de . Determine o ângulo de direção das coordenadas e expresse a força como vetor cartesiano.
Passo 1
O ângulo que é o ângulo diretor da força no eixo e vale e o ângulo diretor que é o ângulo da força no eixo vale agora o ângulo diretor que é para o eixo será calculado pela fórmula:
Substituindo os valores temos:
Passo 2
Agora podemos representar a força como a somatória das forças em cada eixo assim sendo:
Uma vez que a força de está contra o sentido de todos os eixos.