Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.6 - Ex. 69

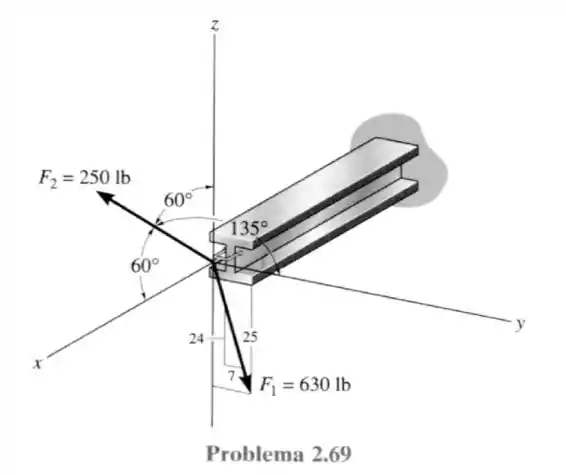
69- A viga está sujeita as duas forças mostradas. Expresse cada força na forma vetorial cartesiana e determine a intensidade e os ângulos diretores coordenados da força resultante.

Passo 1

Os ângulos da força F 2 estão representados na figura logo essa força na forma cartesiana:

F 2 = 250 cos ⁡ 60 i + 250 cos ⁡ 135 j + 250 cos ⁡ 60 k   [ l b ]

Logo:

F 2 = 125 i - 176.78 j + 125   k   [ l b ]

Agora a força F 1 está somente no plano z y e seus ângulos podem ser encontrados pelo triângulo retângulo cujo ângulo com o eixo z   forma os seguintes cossenos e seno:

sin ⁡ θ = 7 25 ;   cos ⁡ θ = 24 25

Logo a representação dessa força será:

F 1 = 630 sin ⁡ θ j - 630 cos ⁡ θ k = 176.4 j - 604.8 k   [ l b ]

Passo 2

A representação vetorial da força resultante será igual a:

F r = F 1 + F 2 = 125 i + - 176.78 + 176.4 j + 125 - 604.8 k

F r = 125 i - 0.38 j - 479.8 k   [ l b ]

Com isso a intensidade da força resultante será:

F r = 125 2 + - 0.38 2 + - 479.8 2 = 495.82   N

Passo 3

Agora podemos encontrar os ângulos diretores da força resultante:

α = cos - 1 ⁡ 125 495.82 = 75.4 °

β = cos - 1 ⁡ - 0.38 495.82 = 90.04 °

γ = cos - 1 ⁡ - 479.8 495.82 = 165.4 °

Resposta

F 1 = 176.4 j - 604.8 k   [ l b ]

F 2 = 125 i - 176.78 j + 125 k   [ l b ]

F r = 125 i - 0.38 j - 479.8 k [ l b ]

F r = 492.82   N

α = 75.4 ° ;     β = 90.04 ° ;     γ = 165.4 °

Ver Outros Exercícios desse livro