66- O mastro está sujeito as três forças mostradas. Determine os ângulos diretores coordenados , , de , de modo que a força resultante que atua sobre o mastro seja
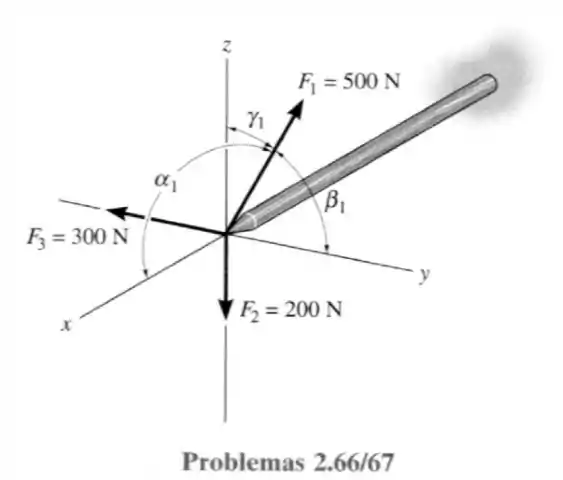
Passo 1
A força pode ser representa por:
E da força :
E a força :
Com isso a força resultante será:
Passo 2
Porém a força resultante dada no enunciado é de logo a força resultante é:
Logo:
O que dá:
Para os outros:
Continuando :