Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 67

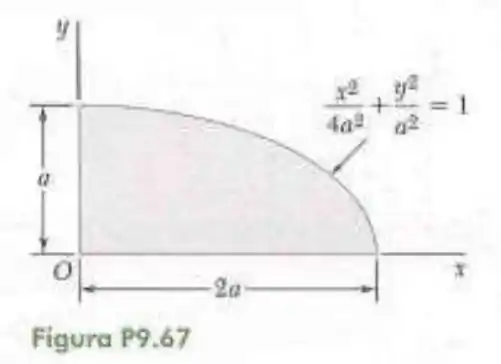
67- Determine por integração direta o produto de inércia da superfície dada em relação aos eixos x e y .

Passo 1

Nessa questão queremos a inércia I x y e para isso precisamos fazer a integral.

I x y = ∫ x y   d A

E pelo elemento de área vertical temos

Onde x varia de 0 até 2 a e y de 0 até a .

Isolando y da equação temos que:

y = a 2 - x 2 4

Passo 2

Logo para resolver essa integral temos que fazer:

I x y = d I ´ x y +   x ¯ y ¯ d A

I x y = d I ´ x y + x y 2   d A

Pois o centro do elemento de área dessa elipse está na metade da altura y e a uma distancia x da origem

Pela simetria nos eixos x e y temos que d I x y ' = 0

Passo 3

Agora temos que saber o tipo de integral que queremos resolver, e para isso vamos pegar a área elementar vertical dessa superfície e isso nos dará:

d A = y   d x

Onde y vale:

y = a 2 - x 2 4

Onde x varia de 0 até a e agora:

I x y = 1 2 ∫ x y 2   d x

I x y = 1 2 ∫ 0 a a 2 x - x 3 4   d x

I x y = 1 2 a 2 x 2 2 - x 4 16 0 a

I x y = 1 2 2 a 4 - a 4 = a 4 2

Resposta

I x y = a 4 2

Ver Outros Exercícios desse livro