Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 69

69- Determine por integração direta o produto de inércia da superfície dada em relação aos eixos x e y .

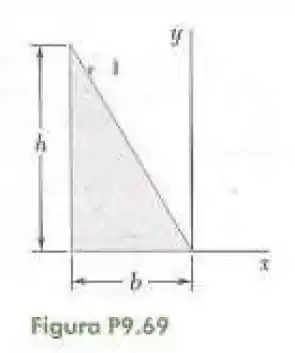
Passo 1

Por ser uma figura simétrica em x e em y então :

d I x y ' = 0

E pelo elemento de área vertical nós temos que:

d A = y   d x

Onde y é a equação da reta inclinada que vai do ponto ( a , b ) até ( - b , - h ) e isso nos dá uma equação da reta igual a:

y = m x + b

b = 0

m = h b

E para esse elemento de área vertical temos que:

x ¯ = x

y ¯ = y 2

Passo 2

Logo a equação de integral será:

I x y = 1 2 ∫ x y × y   d x

Onde y = h b x , e x varia de 0 até - h .

I x y = 1 2 ∫ 0 - b x h 2 b 2 x 2 d x

I x y = h 2 2 b 2 x 4 4 0 - b = h 2 b 2 8

Resposta

I x y = h 2 b 2 8

Ver Outros Exercícios desse livro