Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.6 - Ex. 67
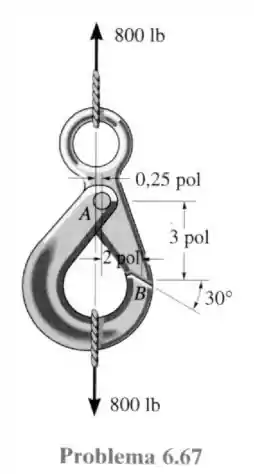
67- O gancho tipo olhal tem um sistema de fechadura tipo ferrolho que sustenta a carga porque duas partes são conectadas por um pino em , que é pressionado contra a superfície lisa em . Determine a força resultante no pino e a força normal em quando o gancho sustenta uma carga de .
Passo 1
Podemos analisar tanto o corpo de cima quanto o corpo de baixo para encontrar as forças que a questão nos pede para encontrar. Vamos utilizar o corpo de cima, o que nos deixará com um sistema de forças equivalente a:
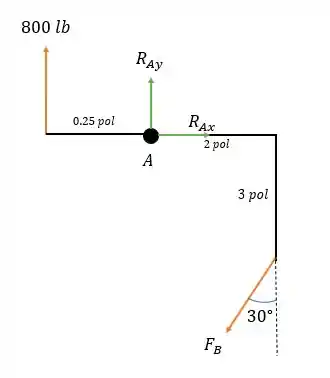
Só nos interessa as distâncias retas até o ponto de interesse. Além do ângulo normal ser sempre em relação a vertical.
Fazendo a somatória dos momentos em temos:
Onde temos que rebater as forças nas horizontal e vertical para conseguirmos calcular o momento.
O sinal só nos diz que o sentido da força está errado. Porém a resultante é essa dai mesmo.
Passo 2
Fazendo a somatória das forças verticais nós encontramos:
Agora para a somatória das forças horizontais:
Tanto o sentido de e de estão ao contrários (bem não da para adivinhar tudo né).
Logo a resultante em será igual a: