Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.6 - Ex. 77
77- Determine os componentes horizontais e verticais das forças nos pinos e e as reações para o apoio fixo da estrutura de três elementos.
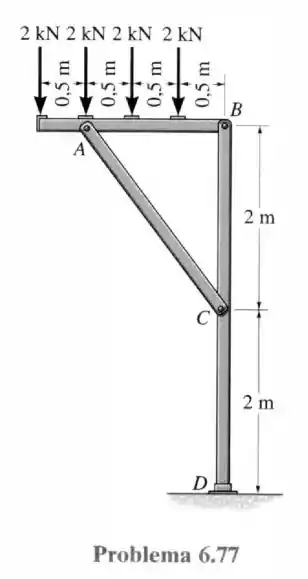
Passo 1
Podemos considerar o apoio como um engaste que possui resistências a duas forças, forças em em e um momento no plano e que pode ser calculada utilizando a estrutura, deixando o diagrama de forças da seguinte forma:
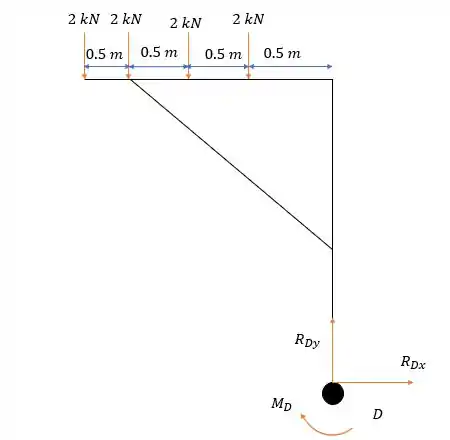
Fazendo a somatória das forças verticais temos:
E fazendo a somatória das forças horizontais:
E a somatória dos momentos em :
Passo 2
Agora vamos só analisar as forças na barra (isso faz com que as forças no pino e apareçam).
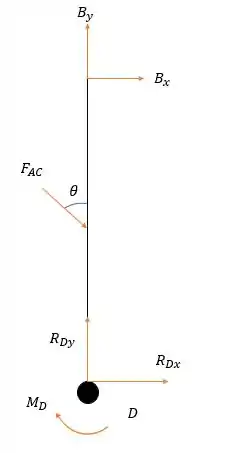
Como sabemos o ângulo que a barra forma com a vertical então é preferível usar a intensidade e não a decomposição, logo:
E as suas decomposições serão:
Componente em apontando da esquerda para a direita e componente em apontando para baixo.
Fazendo a somatória dos momentos (sentido horário positivo) em nós teremos:
Logo as componentes horizontal e vertical no pino serão iguais a:
Agora podemos calcular as reações em fazendo a somatória das forças em e .
Fazendo a somatória das forças horizontais nós temos:
E fazendo a somatória das forças verticais:
Passo 3
Agora falta as forças no pino . Para isso a melhor forma é analisar a barra .
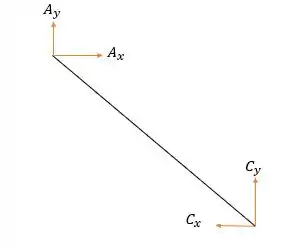
Fazendo a somatória das forças horizontais nós temos:
E fazendo a somatória das forças verticais: