Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.6 - Ex. 79
79- Determine os componentes horizontais e verticais das forças que os pinos em e exercem em seus elementos interligados.
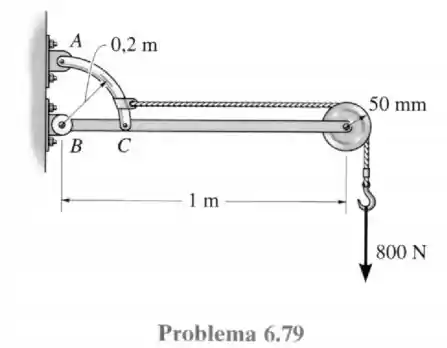
Passo 1
Primeiramente vamos separar a barra e o arco da parede, o que nos dará o seguinte diagrama de forças.
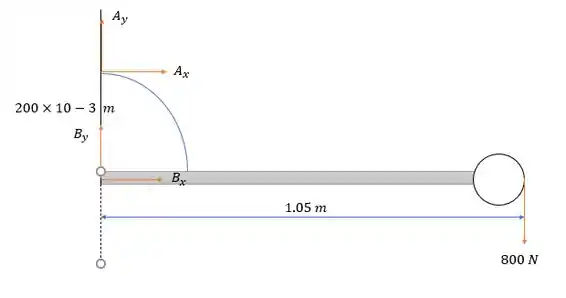
Nesse caso não vamos ter forças em pois ele prende o arco e a barra, logo há ação e reação.
Fazendo a somatória dos momentos em temos:
Logo pela somatória das forças verticais temos:
Agora pela somatória das forças verticais temos:
Passo 2
Agora vamos destacar o arco e verificar as forças que atuam sobre ela.
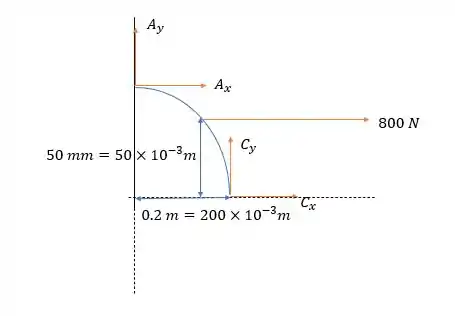
Onde o cabo puxa o arco com uma força de a uma altura de .
Passo 3
Como sabemos a intensidade de vamos fazer a somatória dos momentos em .
Logo será:
Passo 4
Com os valores da reação em nós conseguimos calcular as reações em fazendo a somatória das forças no arco.
Fazendo a somatória das forças horizontais temos:
E agora fazendo a somatória das forças na vertical temos: