68. Determine a força horizontal que atua no cabo da chave de forma que essa força produza um componente de momento ao longo do eixo (eixo ) do conjunto de tubos igual a . Tanto a estrutura de tubos quanto a chave, em , estão no plano . Dica: empregue a análise escalar.
Passo 1
Não se assuste com o termo , pois como só tem uma componente a intensidade é .
Então temos que achar uma força que produza esse momento. Para isso, vamos usar a análise escalar e conseguir achar o valor da força.
A análise escalar é baseada na fórmula:
Onde nesse caso é a distância perpendicular do braço do momento a parti do eixo da linha da força.
Nessa situação podemos notar que a força é perpendicular a chave inglesa (só olhar a figura),
Logo ela só tem a componente em .
Vamos definir também o sentido positivo do momento conforme a regra da mão direita.
Passo 2
Para sabermos o valor do braço de momento, vamos analisar a seguinte figura que provém da figura fornecida pelo enunciado:
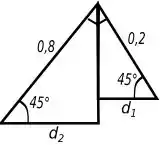
Podemos ver que o braço de momento é soma das bases dos triângulos (tendo os seus dois ângulos inferiores igual a ) as bases dos triângulos são dadas por:
E
Logo o braço total é:
Passo 3
Calculando o momento com o que conseguimos:
Continuando: