Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 68

68- Determine por integração direta o produto de inércia da superfície dada em relação aos eixos x e y .

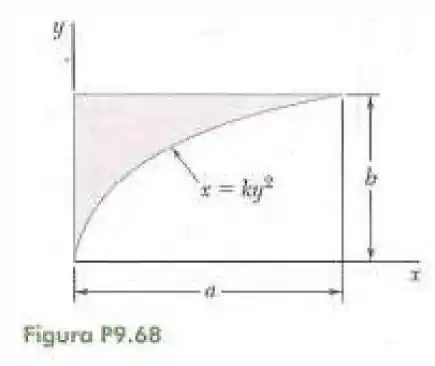
Passo 1

Para encontrar o valor de k vamos aplicar o ponto ( a , b ) que pertence a superfície na sua equação:

a = k b 2

k = a b 2

Agora para fazer a integral vamos pegar o elemento de área horizontal que nos daria a seguinte forma:

d A = x   d y

I x y = d I x y ' + x ¯ y ¯   d A

Onde x ¯ = x 2 e y ¯ = y pelo elemento de área horizontal e d I x y ' pela simetria será zero. E y vai de 0 até b .mm

Passo 2

Fazendo a integral temos:

I x y = 1 2 ∫ 0 b x 2 y   d y

Substituindo o valor de x na equação temos:

I x y = 1 2 ∫ 0 b a b 2 2 y 5   d y

I x y = a 2 2 b 4 y 6 6 0 b

Aplicando o intervalo temos:

I x y = a 2 b 2 12

Resposta

I x y = a 2 b 2 12

Ver Outros Exercícios desse livro