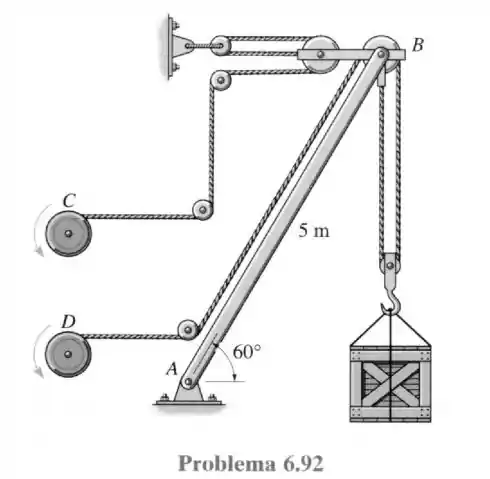
92- O guindaste é conectado por um pino ao pivô em . Determine a maior massa que pode ser sustentada pelo guindaste se a força máxima que o pino em é capaz de suportar é de .
Passo 1
O pino em até pode resistir a forças na horizontal e na vertical e ela só está conectada a barra então a força que passa por essa barra terá que ser o limite máximo resistido pelo pino ou seja:
Agora vamos fazer a somatória das forças que passa na polia .
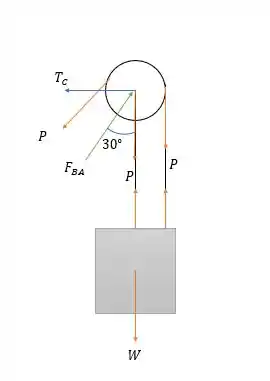
Fazendo a somatória das forças no bloco nós encontramos:
Com
Passo 2
Como a força na articulação é a única que sustenta as forças na polia então não teremos reações no pino, logo fazendo a somatória das forças verticais na polia nós teremos:
Substituindo então e nós teremos:
Como