Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 71
71- Usando o teorema dos eixos paralelos determine o produto de inércia da superfície mostrada na figura em relação aos eixos centroidais e .
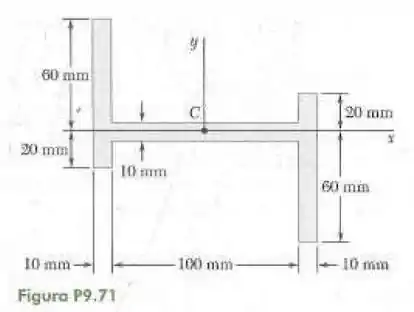
Passo 1
O teorema dos eixos paralelos nos diz que:
Onde é a inércia no centro da figura e no caso do retângulo que é uma figura simétrica, nós podemos dizer de certeza que para todos os retângulos que:
Passo 2
Vamos separar essa superfície em três partes :
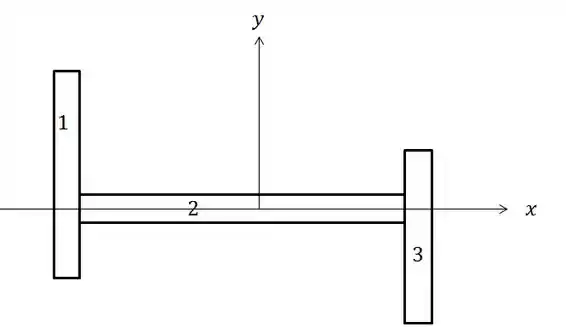
E fazer uma tabela para encontrar o produto de inércia total.
Coma a inércia será a somatória de de todas as superfícies então :