Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 72
72. Determine
(a) as tensões principais e
(b) a tensão de cisalhamento máxima no plano e a tensão normal média. Especifique a orientação do elemento em cada caso.
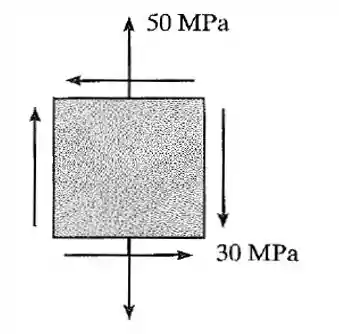
Passo 1
Da figura do enunciado, tiramos que:
A primeira coisa que temos que fazer é determinar a tensão média , através da fórmula abaixo:
E substituindo os valores numéricos correspondentes, chegamos à:
Depois, o próximo passo é achar a tensão máxima de cisalhamento , que é dada por:
Trocando os valores de cada variável, obtemos nossa tensão máxima como:
Passo 2
(a) Obtido a tensão média e a tensão de cisalhamento máxima, todo mundo já tá careca de saber a fórmula das tensões principais, que é dada abaixo:
Esssa relação nos fornece duas tensões uma máxima e outra mínima :
O próximo passo agora, é determinar o nosso ângulo de estado plano , que é dado pela fórmula abaixo:
E o nosso ângulo que queremos para especificar a orientação do elemento é exatamente igual a:
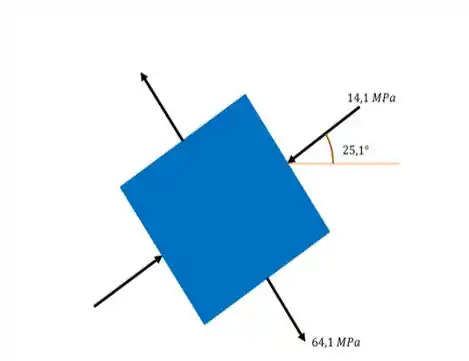
Passo 3
(b) Mas olha só que beleza! Esse item pede a tensão de cisalhamento máximo e a tensão normal média. Acontece que já obtemos elas lá no , como ferramenta para ajudar a calcular as tensões principais. Não acredita!? Pois olha de volta o :
Agora só falta determinar o ângulo de cisalhamento , que é dado através da fórmula abaixo:
Onde substuindo os valores numéricos pertinentes a cada variável, chegamos à:
E o nosso ângulo que queremos para especificar a orientação do elemento é exatamente igual a:
Pra não perder a viagem, vamos fazer também fazer o esboço de nosso querido elemento né; que vai ter a seguinte aparência:
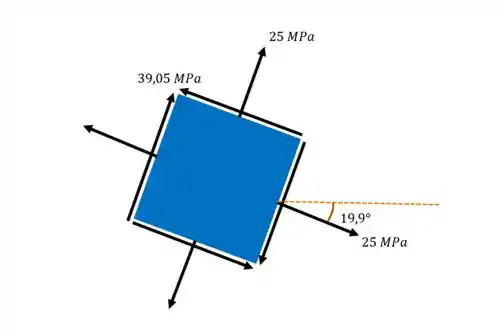
Resposta
(a)
(b)