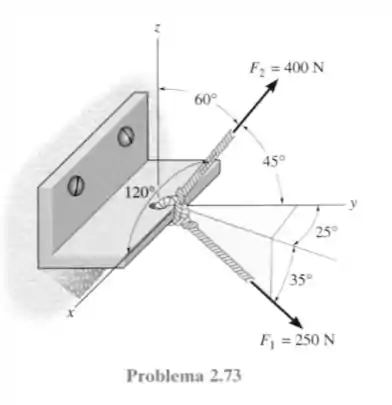
73- O suporte está sujeito as duas forças mostradas. Expresse cada força na forma vetorial cartesiana e depois determine a força resultante , a intensidade e os ângulos diretores coordenados dessa força.
Passo 1
Os ângulos diretores de são as dadas na figura e valem:
Logo sua representação cartesiana é tal que:
Já a força precisa ser rebatida no plano para que possamos encontrar seus componentes nos eixos e . Com esse raciocínio temos a seguinte representação:
Uma vez que a força encontra-se contra o sentido do eixo . Logo:
Passo 2
Assim a força resultante será igual a:
O que resulta em:
O que nos dará uma intensidade igual a:
Passo 3
Assim os ângulos diretivos da força resultante são: