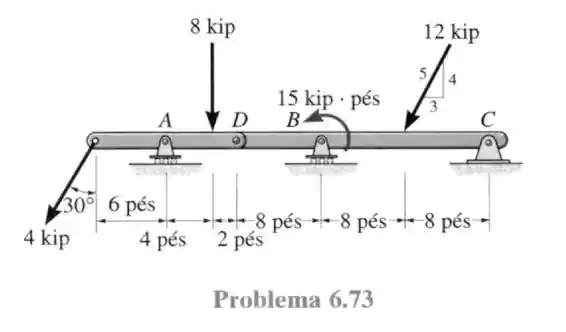
73- A viga composta é apoiada por pinos em e por roletes em e . Existe uma articulação (pino) em . Determine as reações nos apoios. Despreze a espessura da viga.
Passo 1
Vambora pessoal, reforçar o café pra entender mais uma questão.
Note que temos uma viga composta, mas o que seria isso?
Justamente por termos um pino em que junta a barra em duas partes, nós temos dois sistemas isolados e que podem ser analisadas separadamente.
Analisando a viga a esquerda de teremos o seguinte diagrama de forças.
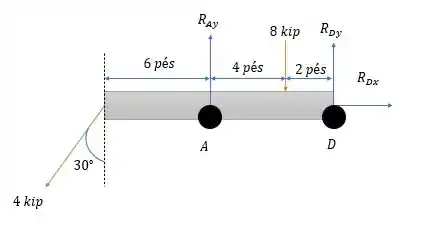
Uma vez que um rolete em só oferece força vertical e o pino oferece forças na vertical e na horizontal.
Fazendo a somatória das forças horizontais ser nula para esse sistema de forças nós teremos:
Agora fazendo a somatória dos momentos em nós teremos (considerando o sentido anti-horário como negativo):
Agora fazendo a somatória das forças verticais nós teremos:
Passo 2
Agora vamos analisar a barra a direita de sabendo que as reações em nessa seção da viga terão sentido contrário a da seção anterior (por uma questão de ação e reação mesmo, não é pra existir nenhuma força resultante em senão o pino sairia da barra né):
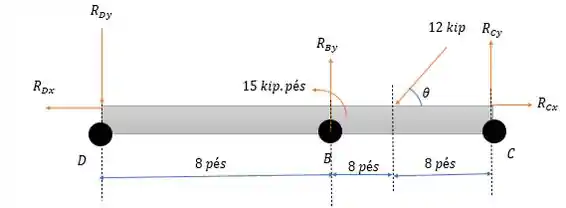
Onde tem as seguintes relações trigonométricas:
Por conta do triângulo 3,4,5 dado no desenho do enunciado.
Fazendo a somatória das forças horizontais nesse sistema de forças temos:
Agora fazendo a somatória dos momentos em temos (assumindo sentido horário positivo):
Logo a somatória das forças verticais nos dará:
E assim chegamos ao final da questão, vamos para mais! A dica nessa questão é sempre que tivermos um pino, lembrar de ação e reação um lado que é ligado a esse pino terá uma força de reação o outro lado terá a força inversa na reação.