Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.6 - Ex. 81

81- Determine a força P na corda e o ângulo θ que o elemento de ligação da polia superior, A B , forma com a vertical. Despreze as massas das polias e do elemento A B . O bloco tem peso de 200   l b e a corda está fixada no pino em B . As polias têm raio r 1 = 2   p o l e r 2 = 1   p o l .

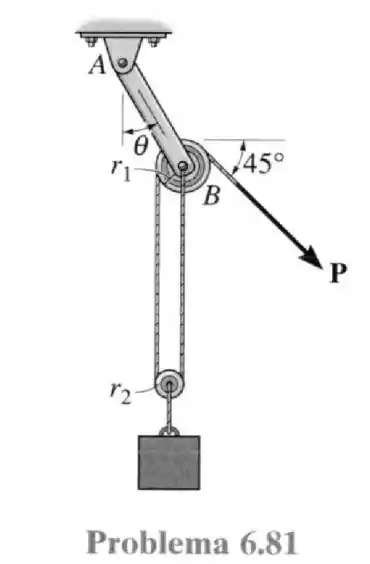
Passo 1

Desenhando o diagrama de forças nos elementos todos nós teremos:

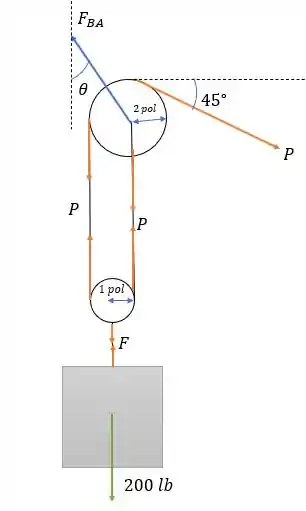
Fazendo a somatória das forças no bloco temos:

F = 200   l b

Fazendo agora a somatória das forças na roldana de raio igual a 1   p o l teremos:

2 P = F

O que dá

P = F 2 = 200 2 = 100   l b

Passo 2

Agora fazendo a somatória das forças horizontais na polia com raio de 2   p o l nós teremos:

P c o s   45 = F B A sin ⁡ θ = 100 cos ⁡ 45

E fazendo a somatória das forças verticais nessa polia nós teremos:

F B A cos ⁡ θ = 2 P + P s i n   45

F B A cos ⁡ θ = 2 × 100 + 100 sin ⁡ 45

Dividindo a primeira equação pela segunda teremos:

tan ⁡ θ = 100 cos ⁡ 45 200 + 100 s i n 45 = 0.2612

Fazendo a arco tangente teremos:

θ = tan - 1 ⁡ 0.2612 = 14.64 °

Resposta

P = 100   l b

θ = 14.64 °

Ver Outros Exercícios desse livro