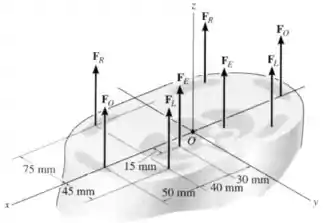
Um modelo biomecânico da região lombar do corpo humano é mostrado na figura. As forças que atuam nos quatro musculares são: para o músculo reto abdominal, para o oblíquo abdominal, para o lumbar latissimus dorsi e para o erector spinae. Essas cargas são simétricas em relação ao plano . Substitua esse sistema de forças paralelas por uma força e momento equivalentes ao sistema que atuam na espinha dorsal, no ponto . Expresse os resultados na forma de vetores cartesianos.

E já que vamos substituir tudo isso por uma única força aplicada na origem, vamos calcular qual era o momento total em relação a inicialmente.

Aqui podemos usar um pouco a nossa intuição pra evitar um produto vetorial complicado;

Como as forças estão “espelhadas” em relação ao eixo , não faz sentido que o sistema vá girar em torno desse eixo.

Além disso, todas as forças são paralelas ao eixo , então também não há como vermos rotação em torno desse eixo.

Por outro lado, dá pra ver que temos muito mais forças em um dos lados do eixo , e apontando na direção perpendicular ao plano , então a rotação dece acontecer em torno de .

Escrevendo essa conclusão matematicamente, temos o seguinte:

Beleza, agora é só multiplicar o módulo de cada força pela sua distância perpendicular até a origem, lembrando de colocar um sinal negativo nas forças que favorecem o sentido horário.

E assim como fizemos antes, vamos multiplicar esse resultado por dois, já que o sistema tem simetria em relação ao plano :

E seguindo a lógica que usamos antes (de que todo o momento aponta no eixo ):