Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.6 - Ex. 78
78- Determine os componentes horizontal e vertical da força em exercida pelo elemento sobre o elemento .
Passo 1
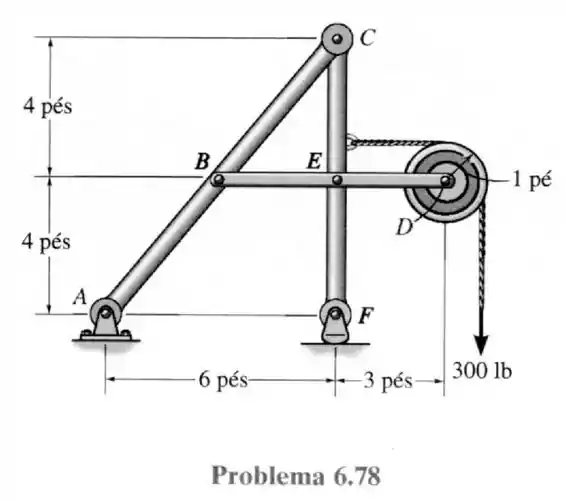
Vamos começar a analisar as reações nos apoios em e pelo momento causado na força ativa de representada na figura.
Fazendo a somatória das forças na horizontal nós temos:
E fazendo a somatória das forças na vertical:
E os momentos em nos dá:
Logo:
Passo 2
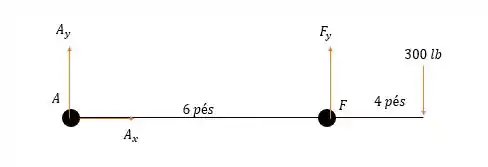
Agora vamos analisar as forças na polia.
Pela somatória das forças na horizontal nós teremos:
E pela somatória das forças verticais:
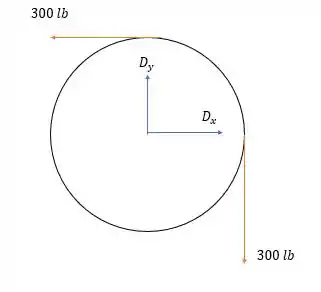
Pode não parecer mas já podemos calcular a força horizontal na junta , para isso vamos analisar as forças na barra .
Onde a polia puxa a barra com uma força igual a , até para anular a força que passa na corda em cima da polia.
Fazendo a somatória dos momentos em nós teremos:
Passo 3
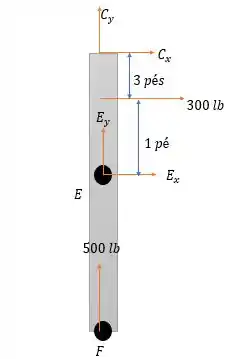
Agora para calcular a componente vertical em vamos analisar o sistema de forças na barra .
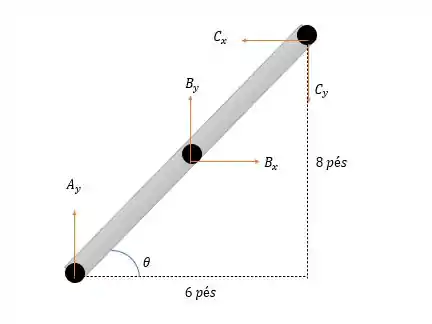
Onde vale:
Então conseguimos ver que está no ponto médio da reta , então o momento das forças em será igual a:
Substituindo os valores que encontramos nós teremos: