87- Determine os componentes horizontais e verticais das forças nos pinos e .
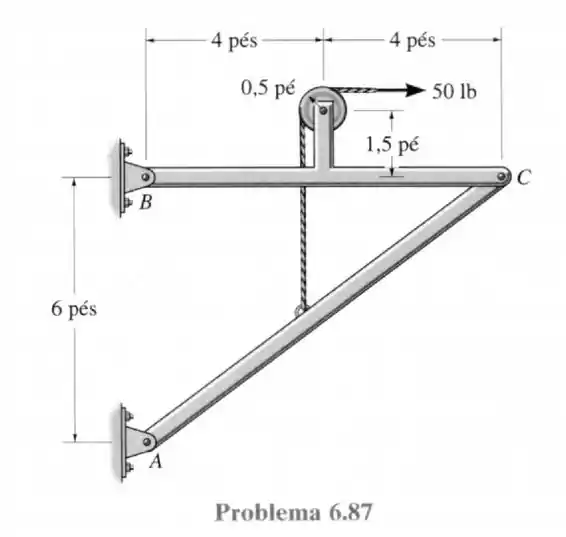
Passo 1
Vamos calcular as reações em e analisando a estrutura toda sabendo que os apoios em e oferecem reações nos dois sentidos.
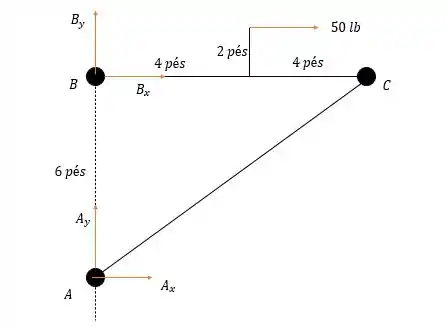
Fazendo a somatória dos momentos em nós temos:
Logo pela somatória das forças horizontais temos:
Agora fazendo a somatória das forças verticais nós temos:
Passo 2
Agora vamos analisar as forças na barra .
Nesse caso a polia tende a empurrar a barra para direita e para baixo.

Sabendo que agora estamos analisando a outra barra que é prendida pelo pino logo suas reações são contrárias.
Fazendo a somatória dos momentos em nós teremos:
Agora fazendo a somatória das forças verticais nós teremos: