95- Determine a força no cabo, sabendo-se que a mola está comprimida em quando o mecanismo está na posição mostrada na figura. A mola tem rigidez .
Passo 1
Como a mola está comprimida em e a constante elástica da mola está em então temos que converter a variação de comprimento da mola para calcular a força elástica no ponto , ficando da seguinte maneira:
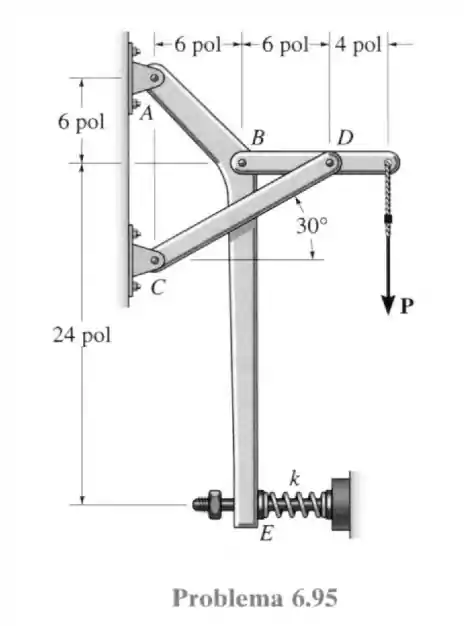
Com essa informação podemos analisar o corpo com a intenção de encontrar as forças em e com isso analisar o corpo para achar a força sacou? Sem mistérios, vamos isolar o corpo da estrutura e ver o seu sistema de forças.
Se a mola está comprimida ela tende a se esticar de novo. Então, bem ela faz a força da direita para a esquerda.
Fazendo a somatória dos momentos em temos:
Passo 2
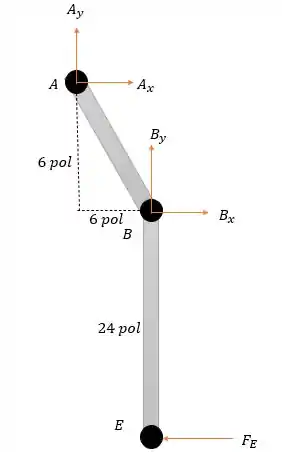
Bem não descobrimos a força em mas conseguimos uma equação, vamos avançar mesmo assim no corpo .
Fazendo a somatória dos momentos em nós temos:
Fazendo a somatória das forças verticais nós encontramos:
E fazendo a somatória das forças horizontais nós teremos:
Passo 3
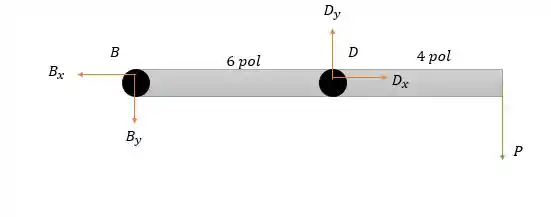
A dica é calcular esse valor de em função de para que possamos matar a questão e como conseguimos atrelar ela em função de logo deveremos ver que a reação dessa barra está na mesma angulação da barra . Ou seja:
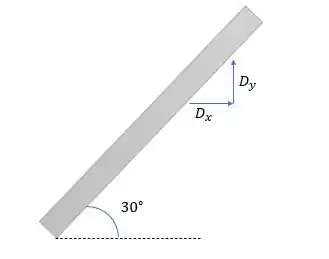
Logo:
Então: