82- A parte dianteira do automóvel deve ser levantada utilizando uma tábua de de comprimento, rígida e sem atrito. O automóvel tem peso de e centro de gravidade em . Determine a posição do suporte para que uma força de aplicada em levante as rodas da frente do automóvel.
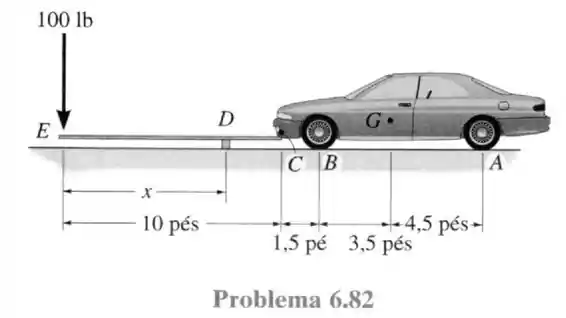
Passo 1
Inicialmente precisamos calcular as reações nas rodas do carro, causadas pela força peso da mesma. Para isso vamos desenhar o diagrama de forças na mesma.
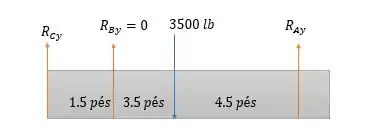
Onde é a ação da tábua no carro e iremos considerar igual a zero pois consideramos o pneu dianteiro do carro levantado já. Fazendo a somatória dos momentos em ser zero nós teremos uma força em igual a:
Passo 2
Agora vamos fazer o diagrama de forças na barra.
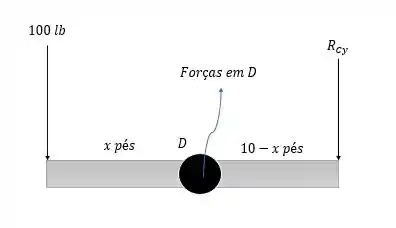
Não esquecendo que o sentido de tem sentido contrário ao do passo anterior, pois aqui é a ação do carro na tábua.
Fazendo a somatória dos momentos em nós teremos: