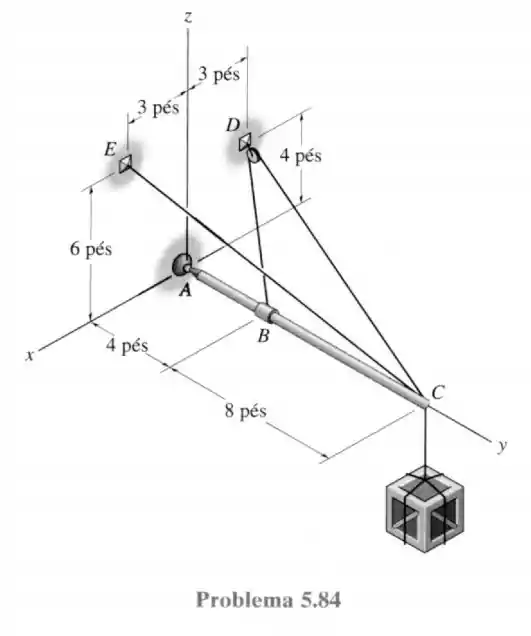
84- A lança é apoiada em por uma junta esférica e por dois cabos e . O cabo é contínuo e passa pela polia em . Calcule a força nos cabos e os componentes de reação em em , se o engradado tem peso de .
Passo 1
A junta esférica oferece reações de forças em todos os eixos e precisamos encontrar as direções das forças em todos os cabos. Para isso vamos encontrar as posições de todos os pontos onde tem as extremidades dos cabos.
Isso faz com que tenhamos os seguintes vetores.
Isso faz com que os vetores unitários sejam:
Logo as forças serão:
Sabendo que a força que passa na polia é a mesma em todo o cabo.
Passo 2
Vamos desenhar o digrama de forças na barra.
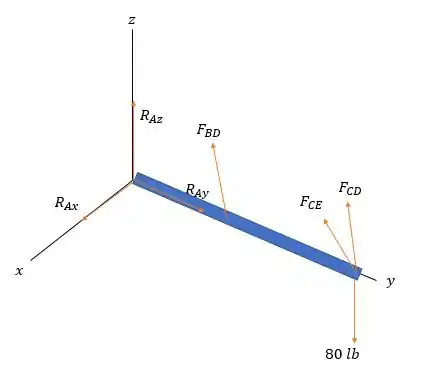
Fazendo a somatória das forças em :
O somatório das forças em :
E a somatória das forças em :
Passo 3
Agora vamos fazer os momentos e como só temos duas forças só precisamos de dois momentos:
Momento em :
Agora fazendo o momento em (por que em não existe)
Dessa forma:
Agora podemos encontrar todas as reações na junta esférica: