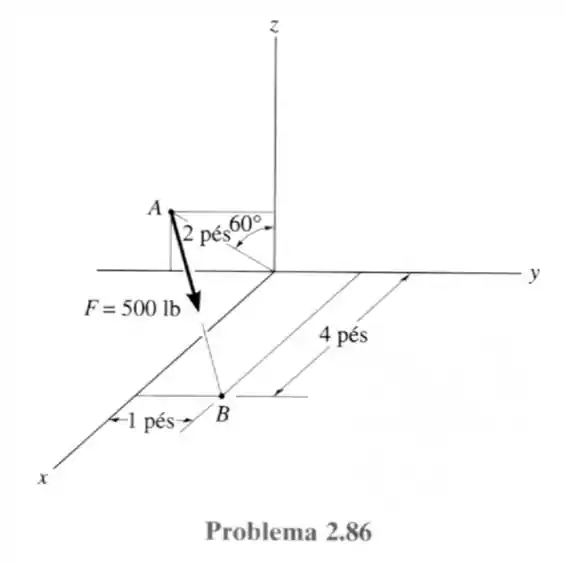
86- Expresse a força como um vetor cartesiano; depois determine seus ângulos diretores ordenados.
Passo 1
O ponto está somente no plano e pode ser representado por:
E o ponto está no plano e essas coordenadas podem ser calculados pela distâncias do ponto até a origem.
Logo:
Passo 2
O sentido do vetor vai de para e com isso o vetor (que dá a direção do vetor) pode ser encontrado por:
A magnitude desse vetor é dado por:
Passo 3
Para podermos calcular o vetor da força precisamos encontrar o vetor unitário de , pois ele que dará a direção do vetor.
O vetor unitário de é , logo:
Como a intensidade da força vale então o vetor direção da força vale:
Passo 4
Para encontrar os ângulos diretores vamos utilizar o vetor unitário por que ele já está no padrão para tal.
Resposta