93- Determine a massa que o cilindro suspenso deve ter para que a tração na corrente em torno da engrenagem de rotação livre seja de . Qual é a intensidade da força resultante no pino ?
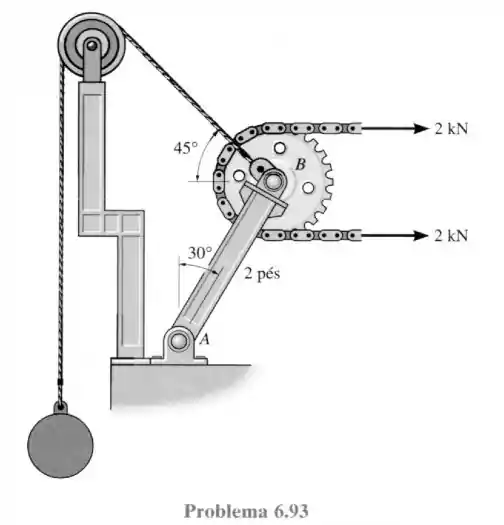
Passo 1
Sabendo que a corrente tende a puxar o pino em para a direita com uma força de e que ela não gera momento em (por pertencer ao mesmo disco) teremos o seguinte sistema de forças no pino em .
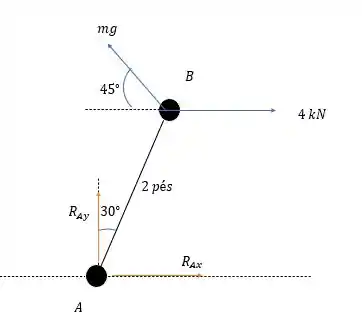
Fazendo a somatória dos momentos em nós teremos:
Onde rebatendo a força na horizontal nós precisaremos da distância entre e na vertical e rebatendo a força na vertical nós precisaremos da distância entre e na horizontal. Ai só adotar qual o sentido do momento (no caso adotei o sentido horário como positivo).
Com isso encontramos:
Como
Passo 2
Agora vamos encontrar a intensidade da reação em que tem a seguinte fórmula:
Fazendo a somatória das forças horizontais nós encontraremos :
E fazendo a somatória das forças verticais nós encontraremos :
Logo a intensidade da reação em será igual a: