Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.6 - Ex. 89
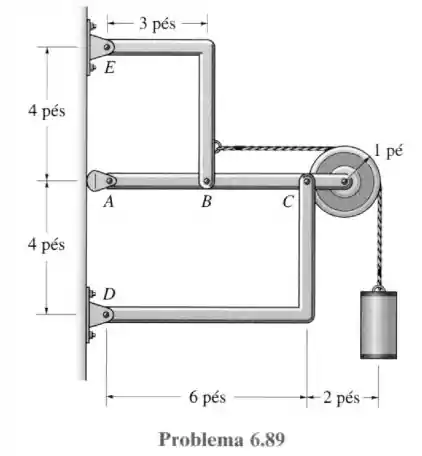
89- Determine os componentes horizontais e verticais das forças em cada pino. O cilindro suspenso tem peso de .
Passo 1
Vamos começar analisando as forças na barra que parecer mais simples e que tiver mais informações, como o apoio em é formado apenas por um rolete (que só faz uma normal com a parede) e temos uma polia que gera forças na extremidade da barra (como se tivesse empurrando ela para baixo e para a esquerda, fazendo com que o sistema de forças nela fique da seguinte forma:
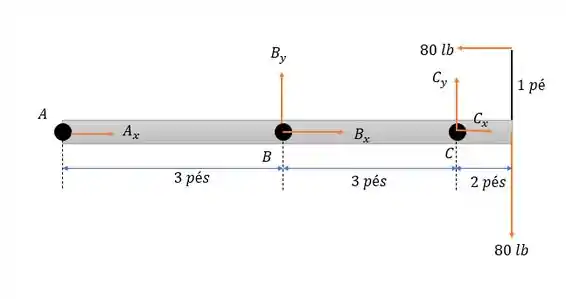
Onde temos que considerar as forças das polias sem a reação da corda horizontal (pois ela está no corpo ). Com isso se fizermos a somatória dos momentos em nós temos:
Dessa forma a somatória das forças verticais serão iguais a:
O que dá:
Agora pela somatória das forças horizontais nós temos:
Passo 2
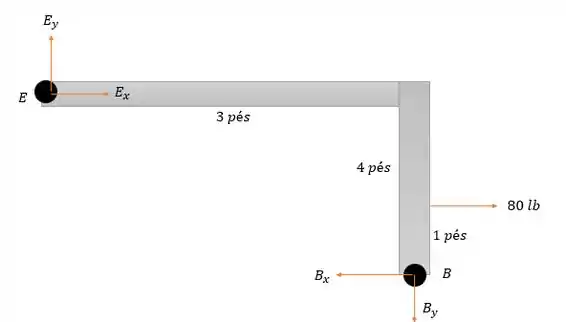
Agora vamos analisar as forças na barra ,
Pela somatória das forças verticais temos que:
Agora fazendo a somatória dos momentos em temos:
E pela somatória das forças horizontais então:
Passo 3
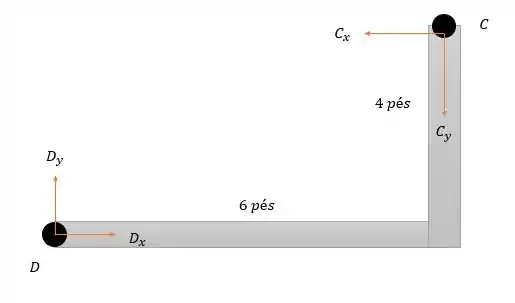
Agora vamos para a outra barra que falta que é o corpo , sabendo que existe a reação causada pela ação da polia (justamente a ação vista no passo ).
Fazendo a somatória das forças em temos:
Agora fazendo a somatória dos momentos em temos:
Pela somatória das forças horizontais temos:
Agora se lembra do passo que fizemos a somatória das forças horizontais que encontramos a equação:
Logo será: