91- Determine os componentes horizontais e verticais das forças que os pinos em e aplicam no elemento da estrutura.
Passo 1
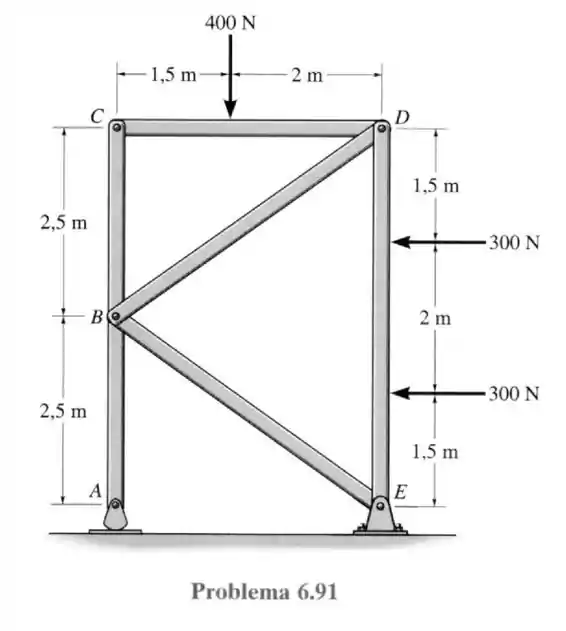
Então pessoal, quando olhamos para as forças na estrutura toda nós devemos considerar as reações nos apoios e (como se tirássemos ele do chão e a partir de agora devemos saber os tipos de reação que estão nos apoios que formam a base). Deixando nosso sistema de forças da seguinte maneira.
Onde o apoio em se assemelha muito a um rolete e a reação em oferece reações nos dois sentidos.
Fazendo a somatória dos momentos em nós teremos a única reação em (considerei o sentido horário como positivo).
Passo 2
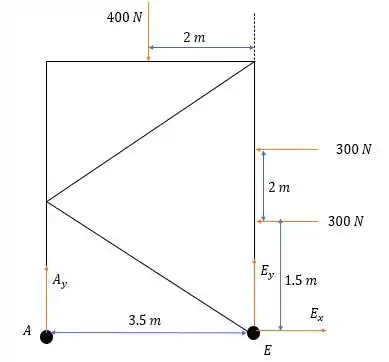
Agora vamos encontrar as forças no pino analisando somente a barra , isso é, vamos destacar essa barra da estrutura (o que faz aparecer somente a força de reação nos pinos e ). Podendo ser desenhado da seguinte forma:
Fazendo a somatória dos momentos em nós teremos:
Logo a força em será igual a:
Passo 3
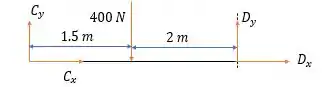
Agora vamos analisar a barra para conseguirmos encontrar outras forças.
Se fizermos a somatória dos momentos em nós teremos:
Agora pela somatória das forças horizontais nessa barra nós teremos:
E pela somatória das forças verticais:
O sinal significa que aponta para baixo e não para cima.