Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.6 - Ex. 76
76- O arco com três dobradiças sustenta as cargas e . Determine os componentes verticais e horizontais das reações nos pinos em e . Considere que .
Passo 1
Como temos dois corpos ligados em vamos analisar um corpo e depois o outro, as forças no pino serão uma força intermediária entre uma e outra.
Começando pelo corpo temos o seguinte diagrama de forças:
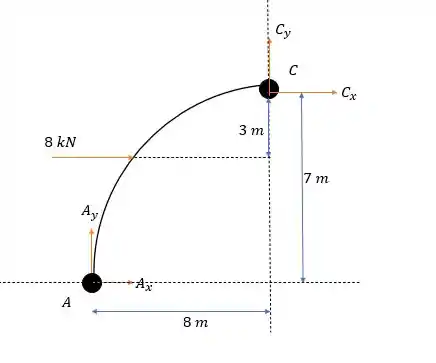
Fazendo a somatória dos momentos em nós teremos:
Isso dá:
Agora a somatória das forças verticais:
E a somatória das forças horizontais:
Passo 2
Agora vamos analisar as forças no corpo .
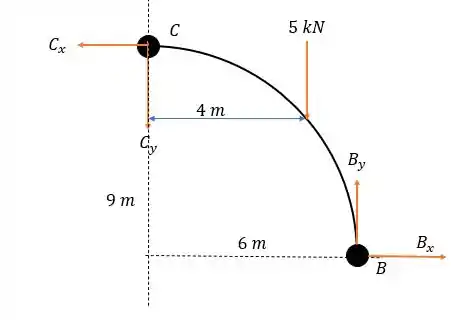
Fazendo a somatória dos momentos em temos:
E a somatória das forças verticais nos dá:
E a somatória das forças horizontais é:
Passo 3
As equações que temos então são as seguintes:
Onde todos os valores estão em . E temos seis equações para seis incógnitas, conseguimos resolver.
Primeiramente vamos eliminar e com o que conhecemos ou seja e .
O que nos dá:
Agora vamos colocar os termos em em relação a , ou seja:
E aplicar esses dois resultados na equação 3:
Se compararmos com a equação temos o sistema:
Que nos dará o seguinte resultado:
Logo:
Com esses valores podemos calcular as reações em mas a questão não pede então deixa para lá.