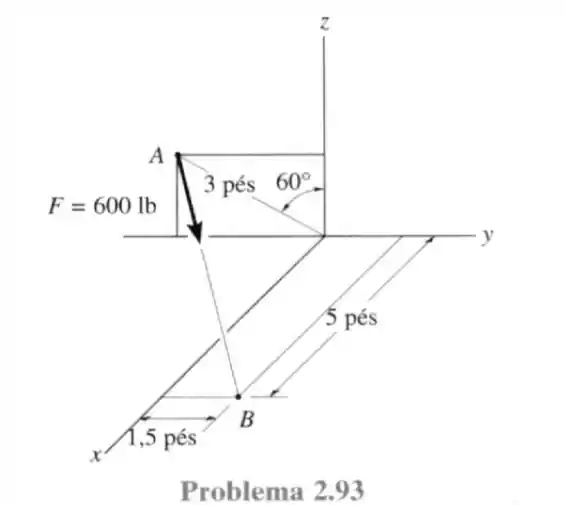
93- Expresse a força como um vetor cartesiano; depois determine seus ângulos diretores coordenados.
Passo 1
Pela figura conseguimos dizer que a posição referente a posição cartesiana vale:
Para a posição de temos:
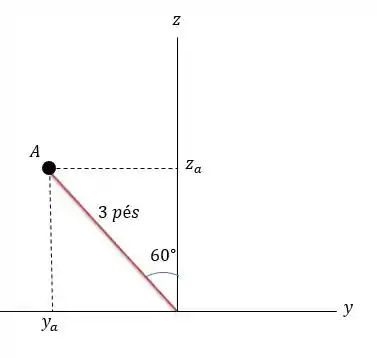
Onde por relações trigonométricas conseguimos encontrar as coordenadas e .
Dessa forma o ponto está no posição cartesiana igual a:
Passo 2
Com o vetor vai de até então temos que diminuir a posição de com a de para encontrar a sua posição cartesiana:
E o comprimento desse vetor será:
Passo 3
Isso nos dará a o seguinte o seguinte vetor unitário:
Como a intensidade da força vale então o vetor força vale:
Passo 4
Para os ângulos diretores vamos utilizar os valores dos eixos no vetor unitário, logo: