Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 59

9.59. O painel mostrado na figura forma a seção transversal de uma calha que está cheia de água até a linha AA’. Voltando à Seção 9.2, determine a altura do ponto de aplicação da resultante das forças hidrostáticas atuantes sobre o painel (o centro de pressões).

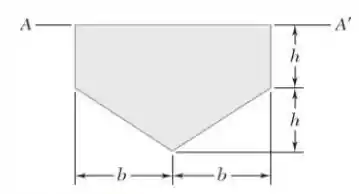
Passo 1

A gente quer calcular a profundidade do ponto de aplicação de resultante das forças, então a gente só precisa calcular a resultante em y. Para isso temos a equação:

y p = I A A ' y → A

O que a gente pode fazer aqui para ficar mais simples é separar a imagem em duas

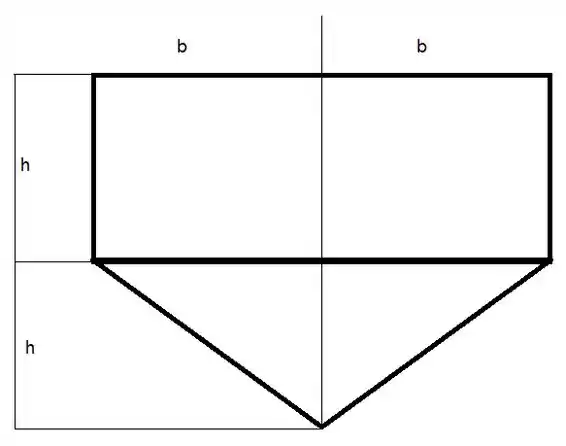
Agora a gente tem o retângulo em cima e o triângulo em baixo.

Podemos fazer isso já que

Y - A = ∑ y - A

Passo 2

Para o retângulo temos:

I A A ' ( 1 ) = 1 3 2 b h 3 = 2 3 b h 3

A = 2 b ⋅ h

y - = h 2

E para o triângulo

A = 1 2 2 b ⋅ h = b ⋅ h

I A A ' ( 2 ) = I - x + A d 2 = 1 36 2 b h 3 + 1 2 ⋅ 2 b ⋅ h 4 3 h 2

Simplificando isso

I A A ' 2 = 11 6 b h 3

y - = 4 3 h

Agora vamos substituir

y p = I A A ' ( 1 ) y → A ( 1 ) + I A A ' ( 2 ) y → A ( 2 )

y p = 2 3 b h 3 h 2 2 b ⋅ h + 11 6 b h 3 4 3 h b ⋅ h

Agora é só simplificar isso

y p = 5 2 b h 3 7 3 b h 2 = 15 14 h

Resposta

y p = 15 14 h

Ver Outros Exercícios desse livro