Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 60

9.60. O painel mostrado na figura forma a seção transversal de uma calha que está cheia de água até a linha AA’. Voltando à Seção 9.2, determine a altura do ponto de aplicação da resultante das forças hidrostáticas atuantes sobre o painel (o centro de pressões).

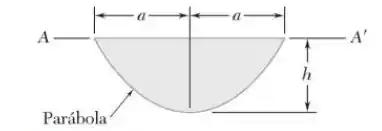
Passo 1

A gente quer calcular a profundidade do ponto de aplicação de resultante das forças, então a gente só precisa calcular a resultante em y. Para isso temos a equação:

y p = I A A ' y → A

Para uma parábola nós temos

y - = 2 5 h

A = 4 3 a h

E para o momento de inércia, nós temos que usar uma diferencial em x, quando pega a diferencial em x de uma parábola, podemos aproximar de um retângulo

d I A A ' = 1 3 h - y 3 d x

Passo 2

A gente pode colocar y em função de h e x, observando a parábola podemos perceber que sua equação é:

y = h a 2 x 2

Isso vai nos ajudar a calcular o momento de inercia

d I A A ' = 1 3 h - h a 2 x 2 3 d x  

Agora a gente tem que integrar

∫ d I A A ' = ∫ 1 3 h - h a 2 x 2 3 d x  

Vamos ter que expandir para ficar mais fácil calcular

I A A ' = ∫ 1 3 h 3 - 3 h 2 x 2 a 2 + 3 h 3 x 4 a 4 - h 3 x 6 a 6 d x

Agora a gente faz integral por integral, a primeira é simples

∫ h 3 d x = h 3 x

Agora a segunda ∫ 3 h 2 x 2 a 2 d x = h 3 x 3 a 2

A terceira ∫ 3 h 3 x 4 a 4 = 3 h 3 x 5 5 a 4

E finalmente

∫ h 3 x 6 a 6 = h 3 x 7 7 a 6

Agora a gente tem o valor dessa integral

I A A ' = 1 3 h 3 x - h 3 x 3 a 2 + 3 h 3 x 5 5 a 4 - h 3 x 7 7 a 6 0 a

I A A ' = 1 3 h 3 a - h 3 a + 3 h 3 a 5 - h 3 a 7 0 a

Então

I A A ' = 32 105 a h 3

Até que deu uma equação bonitinha.

Passo 3

Agora substituímos na formula

y p = 32 105 a h 3 2 3 h ⋅ 4 3 a h

Simplificando isso temos

y p = 4 7 h

Resposta

y p = 4 7 h

Ver Outros Exercícios desse livro