97- Determine as reações nos apoios e para o equilíbrio da viga.
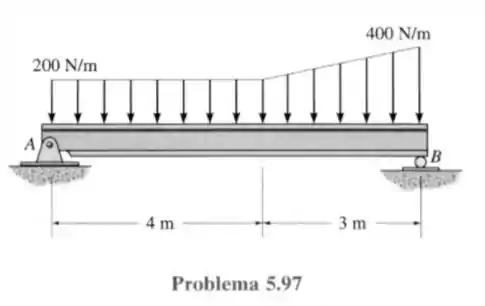
Passo 1
Vamos desenhar as reações e as áreas pertinentes para resolver esse problema.
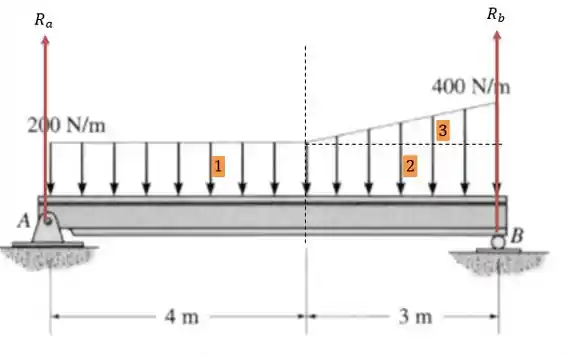
A área do retângulo nos dá a contribuição total da carga dessa região na viga e que será igual a:
E ela se encontra na posição, em relação a igual a:
Já a região contribui com uma força na viga igual a:
E essa força encontra-se numa posição (em relação a ) igual a:
Já a área contribui com uma força na viga igual a sua área, e que vale:
E está numa posição em relação a igual a:
Uma vez que é o centro do triângulo retângulo.
Passo 2
Isso nos dá uma viga equivalente igual a:
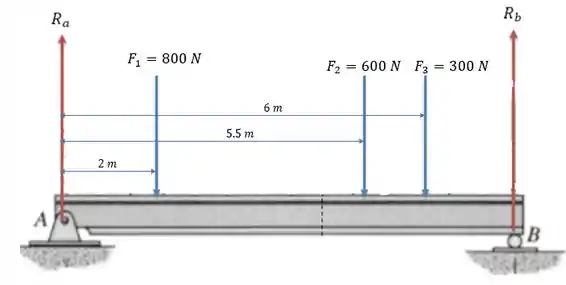
Fazendo a somatória das forças verticais temos:
E fazendo a somatória dos momentos em nos dá:
Logo:
Como não temos forças horizontais então o apoio de segunda ordem em que tem capacidade de suportar cargas horizontais tem reação horizontal