Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.6 - Ex. 98
98- A plataforma de elevação em formato de tesoura consiste em dois conjuntos de elementos cruzados e dois cilindros hidráulicos , localizados simetricamente em cada lado da plataforma. O elevador tem massa uniforme de , com centro de gravidade em ,.A carga de com centro de gravidade em , é centralizada entre cada lado do elevador. Determine as forças em cada um dos cilindros hidráulicos para a condição de equilíbrio. Roletes são colocados em e .
Passo 1
Imagine que tem duas barras e na nossa frente e outra atrás, logo o peso que uma dessas estruturas sustenta é igual a metade da carga e a figura pode estar esquisita pois ué o que que aquele rolete em está fazendo ali? Onde a estrutura está vazia nesse local. Bem na verdade não está o rolete segura verticalmente as cargas do mesmo jeito ok? O que nos dá o sistema de forças.
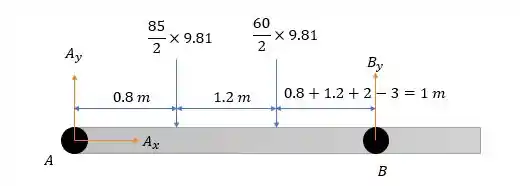
Fazendo a somatória dos momentos em temos:
Logo:
E pela somatória das forças horizontais temos:
Passo 2
Agora vamos para o sistema de forças na barra .
A somatória dos momentos em nos dá:
Substituindo os valores que conhecemos:
Onde será igual a força no cilindro hidráulico.
Passo 3
Agora vamos descobrir as forças verticais nas reações ao analisar o diagrama de forças na estrutura todas.
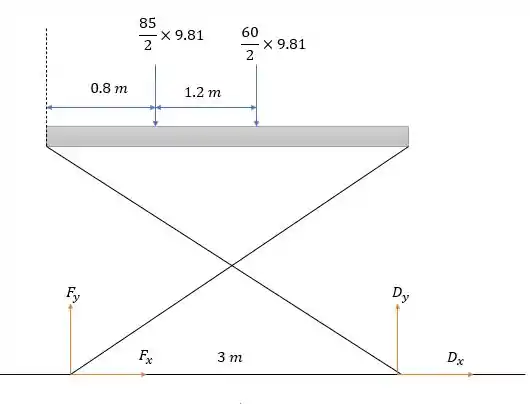
Fazendo a somatória dos momentos em nós temos:
Logo será:
Lembrando que é a força em cada cilindro hidráulico e o sinal nos diz que o sentido dessa força está para o outro lado!